K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
16 tháng 12 2023
Số cuối cùng của tổng là bao nhiêu hả bạn? Bạn nên ghi đầy đủ đề để mọi người hỗ trợ tốt hơn nhé.
30 tháng 3 2016
B=3/2 xin loi nha
vì cách trình bày trên này khó quá, đọc chắc bạn ko hiểu đâu
3 tháng 5 2017
Ta có :
\(A=\dfrac{10^8+2}{10^8-1}=\)\(\dfrac{10^8-1+3}{10^8-1}=\dfrac{10^8-1}{10^8-1}+\dfrac{3}{10^8-1}=1+\dfrac{3}{10^8-1}\)
\(B=\dfrac{10^8}{10^8-3}=\dfrac{10^8-3+3}{10^8-3}=\dfrac{10^8-3}{10^8-3}+\dfrac{3}{10^8-3}=1+\dfrac{3}{10^8-3}\)
Vì \(1+\dfrac{3}{10^8-1}< 1+\dfrac{3}{10^8-3}\Rightarrow A< B\)
CM
5 tháng 1 2020
Đáp án B
Ta xét bài toán tổng quát n tem thư được dán vào n bì thư sao cho có ít nhất 1 bì thư được dán vào tem thư có số trùng với số của bì thư đó
Đánh số các tem thư là T 1 , T 2 ,.., T n và các bì thư B 1 , B 2 ,…, B n . Bài toán được giải quyết bằng nguyên lý phần bù. Lấy hoán vị n phần tử trừ đi trường hợp xếp mà không có tem thư nào được dán cùng số với bì thư.
+ Để giải quyết bài toán không có tem thư nào được dán cùng số với bì thư. Ta xây dựng dãy số f(n) như sau:
Công việc dán n tem thư vào n bì thư sao cho không có bì thư nào được dán vào tem thư có số trùng với số của bì thư đó. Công việc này gồm có 2 bước sau
- Bước 1: dán tem T1 lên 1 bì thư Bj khác B1, có n – 1 cách
- Bước 2: Dán tem thư Tj vào bì thư nào đó, có 2 trường hợp xảy ra như sau:
+ TH1: Tem thư Tj được dán vào bì thư B1. Khi đó còn lại n – 2 tem (khác T1 và Tj) là T2,…,Tj-1, Tj+1,…,Tn phải dán vào n – 2 bì thư (khác B1 và Bj). Quy trình được lặp lại giống như trên. Nên TH này có số cách dán bằng f(n-2)
+ TH2: tem thư Tj không được dán vào bì thư B1
Khi đó các tem là T2,…,Tj-1, Tj, Tj+1,…,Tn sẽ được đem dán vào các bì B1, B2,…,Bj-1, Bj+1,…,Bn (mà tem thư Tj không được dán vào bì thư B1). Thì Tj lúc này bản chất giống như T1, ta đánh số lại Tj º T1. Nghĩa là n – 1 tem T2, …, Tj-1, T1, Tj+1,…,Tn sẽ được đem dán vào n – 1 bì B1, B2,…,Bj-1,Bj+1,…,Bn với việc đánh số giống nhau. Công việc này lại được lập lại như từ ban đầu.
Nên TH này có số cách dán bằng f (n-1)
+ Ta xét dãy u n = f n như sau
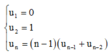
Như vậy kết quả của bài toán: n tem thư được dán vào n bì thư sao cho có ít nhất 1 bì thư được dán vào tem thư có số trùng với số của bì thư đó sẽ là P n - u n
Áp dụng với n = 8, ta được kết quả là 8!-14833=25487.
C
3
21 tháng 3 2016
\(A=\frac{10^8+2}{10^8-1}=\frac{\left(10^8-1\right)+3}{10^8-1}=\frac{10^8-1}{10^8-1}+\frac{3}{10^8-1}=1+\frac{3}{10^8-1}\)
\(B=\frac{10^8}{10^8-3}=\frac{\left(10^8-3\right)+3}{10^8-3}=\frac{10^8-3}{10^8-3}+\frac{3}{10^8-3}=1+\frac{3}{10^8-3}\)
Vì \(1+\frac{3}{10^8-1}<1+\frac{3}{10^8-3}\) nên A < B
21 tháng 3 2016
Ta có :
A = 108 + 2 / 10 8 - 1 = 1 + 3 / 10 8 - 1
B = 108 / 10 8 - 3 = 1 + 3 / 108 - 3
Vì 3/ 108 - 1 < 3 / 108 - 3=> A < B
NT
2
23 tháng 4 2016
-1/8<x/8<1/4
=>-1/8<x/8<2/8
=>-1<x<2
=>x có thể là 0 hoặc 1, nhưng số 0 không thể là tử
=>x=1
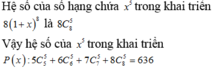
8
8 nhé