K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 6 2017
Gọi biểu thức trên là A
Ta có
\(A=\frac{n^3-2n^2+3}{n-2}\)
\(A=\frac{n^2\left(n-2\right)+3}{n-2}\)
Để \(A\in Z\Leftrightarrow\left(n-2\right)\in U\left(3\right)\)
Vậy ta có:
\(n-2=-3\\ \Rightarrow n=-1\)
\(n-2=-1\\ \Rightarrow n=1\)
\(n-2=1\\ \Rightarrow n=3\)
\(n-2=3\\ \Rightarrow n=5\)
CN
2
31 tháng 10 2021
a: \(P=-\left|5-x\right|+2019\le2019\forall x\)
Dấu '=' xảy ra khi x=5
31 tháng 10 2021
b) \(3^{n+2}-2^{n+2}+3^n-2^n=\left(3^n.3^2+3^n\right)-\left(2^{n-1}.2^3+2^{n-1}.2\right)\)
\(=3^n\left(3^2+1\right)-2^{n-1}\left(2^3+2\right)=3^n.10-2^{n-1}.10\)
\(=10\left(3^n-2^{n-1}\right)⋮10\)
HG
0
26 tháng 11 2017
Bấm vô đây để tham khảo:
Câu hỏi của Phạm Võ Thanh Trúc - Toán lớp 6 - Học toán với OnlineMath
DM
1
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$
DA
2
MH
12 tháng 1 2022
\(\dfrac{x-1}{3}=\dfrac{2-x}{-2}\)
⇔ \(\dfrac{x-1}{3}=\dfrac{x-2}{2}\)
⇔ \(3x-6-2x+2=0\)
⇔ \(x-4=0\)
⇒ \(x=4\)
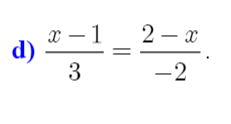
16^n : 2^n = 64
=> (2^4)^n : 2^n = 2^6
=> 2^4.n : 2^n = 2^6
=> 4n - n = 6
=> 3n = 6
=> n =2
k giúp mình
làm ơn