
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\lim\limits_{x\rightarrow-\infty}\dfrac{1+\dfrac{1}{x}}{-\left(m^2+1\right)\sqrt[]{1-\dfrac{4}{x^2}}}=-\dfrac{1}{m^2+1}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\dfrac{1}{m^2+1}\)
\(\Rightarrow\) ĐTHS có 2 tiệm cận ngang
\(\lim\limits_{x\rightarrow2^+}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\dfrac{3}{0}=\infty\)
\(\lim\limits_{x\rightarrow-2^-}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\dfrac{-1}{0}=\infty\)
\(\Rightarrow\) ĐTHS có 2 tiệm cận đứng
Vậy ĐTHS có 4 tiệm cận
tại sao nơi chỗ lim\(_{x->2^+}\) và limx->-2- ở dưới mẫu lại bằng 0 vậy ạ?

\(y'_1=-\dfrac{2}{\left(x-1\right)^2}\) nghịch biến trên R/{1}
\(y'_2=-3x^2+2x-3\) có nghiệm khi y' = 0
\(y'_3=4x^3+4x\) có nghiệm khi y' = 0
Vậy không có hàm số đơn điệu trên R.
đơn điệu trên R là sao bạn? bạn chỉ mk cách nhận bt đc ko?

Đáp án A
Gọi R, h lần lượt là bán kính và chiều cao của khối trụ ban đầu, khi đó thể tích khối trụ ![]()
Khi bán kính tăng lên 2 lần thì thể tích khối trụ mới là ![]() .
.

1/6 tuổi bà là:
6 + 6 = 12 (tuổi)
Tuổi của bà là:
12 : 1/6 = 72 (tuổi)
Đáp số: 72 tuổi
Chúc bạn học tốt!


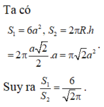
1+689+578-25:6x567=-1094,5