Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\cos60^0=\dfrac{7^2+5^2+a^2}{7\cdot5}=\dfrac{a^2+74}{35}\)
\(\Leftrightarrow a^2+74=17.5\)
hay \(a\in\varnothing\)

a) 1cm + 2cm = 3cm < 4cm
⇒ bộ ba đoạn thẳng 1cm, 2cm, 4cm không thể tạo thành 1 tam giác.
b) 2cm + 3cm = 5cm.
⇒ Bộ ba đoạn thẳng 2cm; 3cm; 5cm không lập thành tam giác.
c) Ta có 3cm + 4cm = 7cm > 5cm.
Do đó bộ đoạn thẳng 3cm, 4cm, 5cm có thể thành 3 cạnh của tam giác.
Cách dựng tam giác có ba độ dài 3cm, 4cm, 5cm :
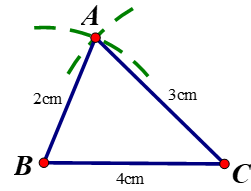
- Vẽ BC = 4cm
- Dựng đường tròn tâm B bán kính 2cm ; đường tròn tâm C bán kính 3cm. Hai đường tròn cắt nhau tại A. Nối AB, AC ta được tam giác cần dựng.

gọi cạnh góc vuông là x(m) (x>0)
a/ Áp dụng định lí Pytago ta có 2x2=4<=>x2=2<=>x=\(\sqrt{2}\left(m\right)\)
b/Áp dụng định lí Pytago ta có 2x2=18<=>x2=9<=>x=3(m)
gọi độ dài cạnh thứ ba là x
Theo đề, ta có:
\(\cos120=\dfrac{5^2+6^2+x^2}{2\cdot5\cdot6}=\dfrac{x^2+61}{60}\)
\(\Leftrightarrow x^2+61=-30\)(vô lý)
- Chắc bạn này học lớp 7 nâng cao :)