Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

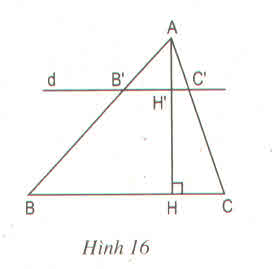
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313BC
=>SAB’C’= (1212AH.BC)1919
mà SABC= 1212AH.BC = 67,5 cm2
Vậy SAB’C’= 1919.67,5= 7,5 cm2

A B C H E F M N
Theo tính chất đường thẳng song song :
\(AK=KI=IH\)( gt )
=> AE = EM = MB
=> AF = FN = NC
Theo bài ra ta có : \(\frac{MN}{BC}=\frac{AM}{MB}=\frac{2MB}{MB}=2\)cm
\(\frac{EF}{BC}=\frac{AE}{EB}=\frac{AE}{2AE}=\frac{1}{2}\)cm
hay \(2EF=BC\)(*)
Ta có : \(S_{ABC}=\frac{1}{2}AH.BC=90\)( gt )
\(\Delta AMN\)có EF là đường trung bình ( AE = EM ; AF = FN )
Suy ra : EF // MN và EF = 1/2 MN
Ta có : \(S_{MNEF}=\frac{\left(EF+MN\right).IK}{2}\)mà \(IK=\frac{1}{3}AH\)
\(=\frac{\left(EF+MN\right).\frac{AH}{3}}{2}=\frac{\left(EF+2EF\right).\frac{AH}{3}}{2}\)
\(=\frac{EF.AH}{2}\)mà \(2EF=BC\)cmt (*)
\(=\frac{\frac{BC}{2}.AH}{2}=\frac{BC.AH}{4}\)
Vậy \(S_{MNEF}=\frac{180}{4}=45\)cm2

a) Ta có : d // BC
=> B'C' // BC
Xét \(\Delta AB'H'\)và \(\Delta ABH\)( B'H' // BH )
Theo hệ quả của định lý Ta-lét
=> \(\frac{AB'}{AB}=\frac{AH'}{AH}\)(1)
Xét \(\Delta AB'C'\) và \(\Delta ABC\)( B'C' // BC )
Theo hệ quả của định lý Ta-lét
=> \(\frac{AB'}{AB}=\frac{B'C'}{BC}\)(2)
Từ (1) và (2)
=> \(\frac{AH'}{AH}=\frac{B'C'}{BC}\)( ĐPCM )
b) \(\frac{SAB'C'}{SABC}=\frac{\frac{1}{2}AH'.B'C'}{\frac{1}{2}AH.BC}=\frac{AH'}{AH}.\frac{B'C'}{BC}=\frac{1}{3}.\frac{1}{3}=\frac{1}{9}\)
=> \(SAB'C'=\frac{1}{9}\Rightarrow SAB'C'=\frac{SABC}{9}=\frac{67,5}{9}=7,5\left(cm^2\right)\)

Cậu tự vẽ hình nhá
a) Do D đối xứng với H qua đoạn AB nên tam giác ADH cân tại A
Tam giác ADH có AB là đường cao đồng thời là phân giác
=> góc DAB = góc HAB
Tương tự với tam giác AHE => góc HAC = góc EAC
Ta có :
góc DAE = (góc DAH) + (góc HAE) = 2.(góc BAH) + 2.(góc HAC) = 2.(góc BAH + góc HAC) = 2.90 = 180
=> D,A,E thẳng hàng
Nhận thấy
Tam giác AHC đối xứng với tam giác AEC qua đoạn thẳng AC => góc AHC = góc AEC = 900 (1)
Tương tự , ta cũng có : góc BHA = góc BDA = 900 (2)
Từ (1) và (2) => BD // EC (do 2 góc trong cùng phía bù nhau)
b) Ta có : tam giác BHA đồng dạng với tam giác AHC
Suy ra tỷ lệ \(\frac{BH}{AH}=\frac{AH}{HC}\Leftrightarrow AH^2=BH.HC\)
Mà BH = BD , HC = CE
=> \(AH^2=BD.CE\)
<=> \(4AH^2=4BD.CE\)
<=> \(\left(2AH\right)^2=4BD.CE\) (Do AD = AH = AE)
<=> \(DE^2=4BD.CE\)