Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mình cho bạn cái này thử vào áp dụng nhé:
Wđ = n Wt => \(x =\pm {A \over \sqrt{n+1}}\)
\(W_đ=W_t\)
\(\Rightarrow W = W_đ+W_t = 2W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=2.\dfrac{1}{2}kx^2\)
\(\Rightarrow x = \pm\dfrac{A}{\sqrt 2}=\pm2\sqrt 2\) (cm)

Đáp án B
Phương pháp: Sử dụng công thức tính cơ năng, thế năng và định luật bảo toàn cơ năng của con lắc lò xo dao động điều hoà
Cách giải:
Khi động năng bằng thế năng thì:
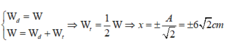

Đáp án A
HD: Trong dao động điều hòa, vật có động năng bằng thế năng tại vị trí A= ± A 2 2

Khoảng thời gian ngắn nhất giữa hai lần liên tiếp vật vật đi qua vị trí có li độ
![]()
+ Lực kéo cực đại của lò xo tác dụng và điểm có định là
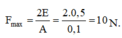
+ Vậy khoảng thời gian ngắn nhất để lò xo kéo điểm cố định một lực 5 N là
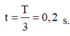
Đáp án D

Chọn đáp án D.
Theo bài:
W d 1 = 2 W t 1 ⇒ 1 3 = W t W = x A 2 = 3 A 2 ⇒ A 2 = 27
Lúc li độ bằng 1cm thì
W t 2 W = 1 A 2 = 1 27 ⇒ W d 2 = 26 W t 2
Vậy so với thế năng đàn hồi của lò xo thì động năng của vật lớn gấp 2 lần

13. Một con lắc lò xo dao động với biên độ 5cm. Xác định li độ của vật để thế năng của vật bằng động năng của nó.
Li độ của vật để thế năng của vật bằng động năng của nó
\(\left\{{}\begin{matrix}W_d=W_t\\W_d+W_t=W\end{matrix}\right.\)=> \(W_t=\dfrac{W}{2}\)
\(\dfrac{1}{2}kx^2=\dfrac{1}{2}.\dfrac{1}{2}kA^2\)
\(\Rightarrow x=\pm\dfrac{A}{\sqrt{2}}\)
12. Một con lắc lò xo dao động với biên độ 10cm. Xác định li độ của vật để thế năng của vật bằng 3 động năng của nó.
\(W=W_d+W_t\)
\(\Leftrightarrow\dfrac{1}{2}kA^2=3W_t+W_t\)
\(\Leftrightarrow\dfrac{1}{2}kA^2=4W_t=4\dfrac{1}{2}kx^2\)
\(\Rightarrow x=\pm\dfrac{A}{2}\)