K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
23 tháng 11 2018
Lời giải:
Xếp $12$ học sinh gồm $7$ nam, $5$ nữ theo hàng dọc ta có \(12!\) cách xếp
Trươc tiên, chọn 1 bạn là nam đứng đầu hàng ta có $7$ cách chọn
Chọn 1 bạn nam đứng cuối hàng ta có $6$ cách chọn
$10$ bạn còn lại xếp ở bên trong ta có \(10!\) cách xếp
Do đó số kết cục thuận lợi: \(7.6.10!\)
Vậy xác suất để người đứng hàng đầu và cuối đều là nam là:
\(P(A)=\frac{7.6.10!}{12!}=\frac{7}{22}\)
Đáp án C
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2019
S A B C D M
\(MA=2a-x\) ;\(MB^2=MA^2+AB^2\); \(MC^2=MA^2+AC^2\)
\(MD^2=MA^2+AD^2\)
\(\Rightarrow MA^2+MB^2+MC^2+MD^2=4MA^2+AB^2+AC^2+AD^2\)
Do đáy là nửa lục giác đều:
\(\Rightarrow\widehat{ABC}=120^0\Rightarrow AC=\sqrt{AB^2+BC^2-2AB.BC.cos120}=a\sqrt{3}\)
\(AD=2BC=2a\)
\(\Rightarrow4\left(2a-x\right)^2+a^2+3a^2+4a^2=12a^2\)
\(\Leftrightarrow\left(2a-x\right)^2=a^2\Rightarrow x=a\)
b/ Nói chung là tìm tâm mặt cầu ngoại tiếp chóp
Gọi I là trung điểm AD \(\Rightarrow I\) là tâm lục giác đều
\(\Rightarrow IA=IB=IC=ID\)
Trong mặt phẳng \(\left(SAD\right)\), qua I kẻ đường thẳng d song song SA \(\Rightarrow\) mọi điểm trên d đều cách đều 4 đỉnh của đa giác đáy
Gọi N là trung điểm SA, trong mặt phẳng (SAD), qua N kẻ đường thẳng d' vuông góc SA (hay song song AD) cắt d tại K \(\Rightarrow K\) là điểm cần tìm
c/ Theo tính chất lục giác đều ta có \(AB\perp BD\)
\(\Rightarrow BD\perp\left(SAB\right)\)
Từ A kẻ \(AH\perp SB\Rightarrow AH\perp\left(SBD\right)\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
Áp dụng hệ thức lượng:
\(\frac{1}{AH^2}=\frac{1}{SA^2}+\frac{1}{AB^2}\Rightarrow AH=\frac{SA.AB}{\sqrt{SA^2+AB^2}}=\frac{2a\sqrt{5}}{5}\)
CM
4 tháng 12 2017
Đáp án : A
Phương án 1: Chọn 1 học sinh giỏi lớp 11A có 25 cách chọn.
Phương án 2: Chọn 1 học sinh giỏi lớp 12A có 20 cách chọn.
Theo quy tắc cộng; có 25+20=45 cách chọn.
CM
5 tháng 10 2017
Chọn D
Vì mỗi học sinh lớp 12A được đăng kí 1 hoặc 2 tiết mục trong số 3 tiết mục văn nghệ nên số cách lựa chọn tiết mục văn nghệ của mỗi học sinh là: C 3 1 + C 3 2 = 6.
Lớp 12A có 44 học sinh đều tham gia văn nghệ nên số cách để lớp lựa chọn là: 6 44 .
CM
26 tháng 5 2019
Đáp án A.
Gọi r và h lần lượt là bán kính đáy và chiều cao của hình trụ. Khi đó r = a.
Thiết diện qua trục của hình trụ là một hình chữ nhật có các kích thước lần lượt là h và 2r. Từ giả thiết ta có:
2(h + 2r) = 12a ⇔ h = 6a - 2r = 4a
Vậy thể tích khối trụ là: 
(đvtt).
CM
19 tháng 5 2019
Đáp án C
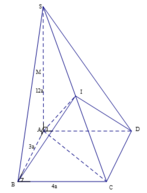
Gọi I là trung điểm SC
Tam giác SAC vuông tại A, ta có: IA = IS = IC
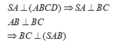
=> ∆ SBC vuông tại B, ta có IB = IS = IC
Tương tự ta có ID = IS = IC
Vậy I là tâm mặt cầu ngoại tiếp hình chóp và bán kính bằng 1 2 SC
Tam giác ABC vuông tại B, ta có: AC = 
Tam giác SAC vuông tại A, ta có SC = 
Vậy bán kính đường tròn ngoại tiếp hình chóp là: R = 13 a 2
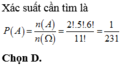
12a+111,25=578,62
<=>12a=467,37
<=>a=38,9475