
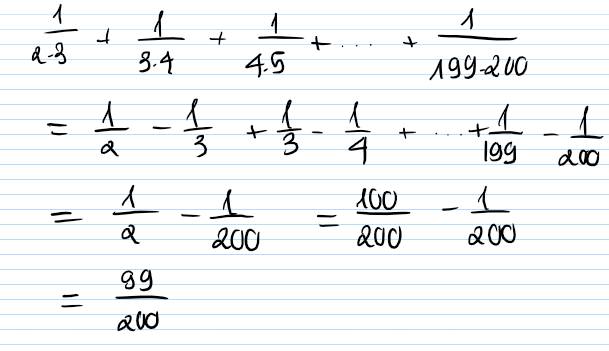
Tinh nhanh nhe
">Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

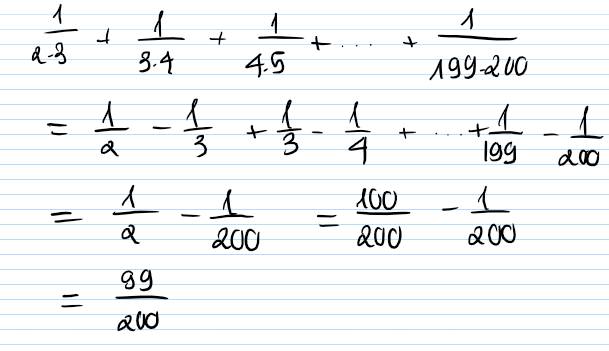

1/2.3+1/3.4+1/4.5+...+1/380
=1/2.3+1/3.4+1/4.5+...+1/19.20
=1/2-1/3+1/3-1/4+1/4-1/5+...+1/19-1/20
=1/2-1/20
=9/20
tick nha bn cám ơn

\(\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+....+\frac{1}{200.201}\)
=\(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+....+\frac{1}{200}-\frac{1}{201}\)
=\(\frac{1}{2}-\frac{1}{201}\)
=\(\frac{199}{402}\)
\(\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+...+\frac{1}{200.201}\)
\(=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{200}-\frac{1}{201}\)
\(=\frac{1}{2}-\frac{1}{201}=\frac{199}{402}\)

\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+.....+\frac{1}{99.100}\)
= \(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+....+\frac{1}{99}-\frac{1}{100}\)
= \(1-\frac{1}{100}\)
\(=\frac{99}{100}\)
\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(=1-\frac{1}{100}\)
\(=\frac{99}{100}\)
thấy đúng thì k cho mk nha mấy bạn

bài A: áp dụng công thức: 1 + 2 + 3 + ... + n = n x (n + 1) : 2 tính được 5050
bài B: áp dụng công thức: \(\frac{1}{n\left(n+1\right)}=\frac{1}{n}-\frac{1}{n+1}\) rồi triệt tiêu gần hết, qui đồng mẫu số tính được B = 99/100
A = 1 + 2 + 3 + 4 + 5 + ... + 99 + 100
= ( 100 + 1 ) x 100 : 2 = 5050
Vậy A = 5050
\(B=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}+...+\frac{1}{99.100}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+...+\frac{1}{99}-\frac{1}{100}\)
\(=1-\frac{1}{100}\)
\(=\frac{99}{100}\)
Vậy \(B=\frac{99}{100}\)
Học tốt #

\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(=1-\frac{1}{100}\)
\(=\frac{100}{100}-\frac{1}{100}\)
\(=\frac{99}{100}\)

\(\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+...+\frac{1}{38\cdot39}+\frac{1}{39.40}\)
\(=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{38}-\frac{1}{39}+\frac{1}{39}-\frac{1}{40}\)
\(\frac{1}{2}-\frac{1}{40}\)
= 0,475

A=1.2+2.3+3.4+4.5+...+99.100
=>3A=1.2.3+2.3.3+3.4.3+4.5.3+...+99.100.3
=1.2.3+2.3.(4-1)+3.4.(5-2)+4.5.(6-3)+...+99.100.(101-98)
=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+4.5.6-3.4.5+...+99.100.101-98.99.100
=1.2.3-1.2.3+2.3.4-2.3.4+3.4.5-3.4.5+4.5.6-4.5.6+...+99.100.101
=99.100.101=999900
=>A=999900:3=333300
Vậy A=333300