Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D N M E
a, kẻ AM cắt CD tại E
xét tam giác AMB và tam giác EMD có : góc AMB = góc EMD (đối đỉnh)
DM = MB do M là trung điểm của BD (gt)
góc ABM = góc MDE (so le trong AB // DC)
=> tam giác AMB = tam giác EMD (g-c-g) (1)
=> AM = ME (đn) có M nằm giữa A và E
=> M là trung điểm của AE
N là trugn điểm của AC (gt) ; xét tam giác AEC
=> MN là đường trung bình của tam giác AEC (đn) (2)
=> MN // EC (Đl)
CE // AB
=> MN // AB
b, (2) => MN = EC/2
EC = CD - DE
=> MN = (CD - DE) : 2
(1) => DE = AB
=> MN = (CD - AB) : 2

Trước tiên kẻ AM cắt CD tại I
Ta xét tam giác AMB và IMD
Hai tam giác đó bằng nhau vì MB=MD (gt) và góc AMB=IMD (đđ) và góc ABM=IDM (so le trong vì AB//CD)
Vì vậy mà AB=ID và MA=MI
Xét tam giác AIC có MA=MI và NA=NC nên MN là đường trung bình của tam giác AIC nên MN//CI và MN=(1/2)CI
Do CI=CD-ID cũng như CI=CD-AB (do AB=ID cmt) và MN=(1/2)CI
nên MN=(1/2)(CD-AB)

Lời giải
a)
Kẻ đường thẳng d qua M // với hai đáy
cắt AD tại P cắt BC tại Q cắt AC tại N'
Ta c/m N trùng N'
xét \(\Delta_{DBC}\) có MQ là đường trung bình tam giác => BQ=QC
PQ//DC => PQ là đường TB của Hình Thang ABCD => P là trung điểm của AD
xét \(\Delta_{DAC}\) có PQ là đường trung bình =>AN'=N'C
=> N' trùng N => MN //AB//CD=> dpcm
b)
???

P là trung điểm của AD, N là trung điểm của AC \(\Rightarrow\) PN // CD ( tính chất đường trung bình) (1)
P là trung điểm của AD, M là trung điểm của BD \(\Rightarrow\) PM // AB (tính chất đường trung bình) (2) Lại có AB // CD \(\Rightarrow\) PM // PN // AB (3)
Từ (1),(2),(3) \(\Rightarrow\)P,M,N thẳng hàng và MN // AB
b) Ta có PN, PM lần lượt là dường trung bình của CD và AB
\(\Rightarrow\) \(PN=\) \(\frac{1}{2}CD\), \(PM=\)\(\frac{1}{2}AB\)
Mà \(PN-PM=MN\) \(\Rightarrow\) \(MN=\frac{1}{2}CD-\frac{1}{2}AB=\frac{CD-AB}{2}\left(dpcm\right)\)

a. Gọi P là trung điểm của AD, nối PM
Trong ΔDAB ta có:
Suy ra:
Suy ra: PM // AB (Định lí đảo của định lí Ta-lét) (1)
Trong ΔACD, ta có
Suy ra:
Suy ra: PN // CD (định lí đảo định lí Ta-lét) (2)
Từ (1) và (2) và theo tiên đề Ơ-clít suy ra P, M, N thẳng hàng.
Vậy MN // CD hay MN // AB.
b. Vì PM là đường trung bình của tam giác DAB nên:
PM = AB/2 (tính chất đường trung bình tam giác)
Vì PN là đường trung bình của tam giác ΔACD nên:
PN = CD/2 (tính chất đường trung hình tam giác)
Mà PN = PM + MN
Suy ra: MN = PN – PM = CD/2 - AB/2 = (CD-AB)/2

Vì PM là đường trung bình của tam giác DAB nên:
PM = AB/2 (tính chất đường trung bình tam giác)
Vì PN là đường trung bình của tam giác ΔACD nên:
PN = CD/2 (tính chất đường trung hình tam giác)
Mà PN = PM + MN
Suy ra: MN = PN – PM = CD/2 - AB/2 = (CD-AB)/2

Gọi P là trung điểm của AD, nối PM
Trong ΔDAB ta có: 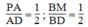
Suy ra: 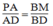
Suy ra: PM // AB (Định lí đảo của định lí Ta-lét) (1)
Trong
△
ACD, ta có 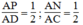
Suy ra: 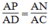
Suy ra: PN // CD (định lí đảo định lí Ta-lét) (2)
Từ (1) và (2) và theo tiên đề Ơ-clít suy ra P, M, N thẳng hàng.
Vậy MN // CD hay MN // AB.

a: Gọi K là trung điểm của BC
Xét ΔBDC có BN/BD=BK/BC
nên KN//DC và KN=1/2DC
Xét ΔCAB có CM/CA=CK/CB
nên MK//AB và MK=1/2AB
=>MK//DC
mà KN//DC
nên K,N,M thẳng hàng
=>MN//AB
b: MN=NK-MK=1/2(CD-AB)



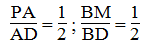
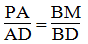
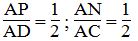
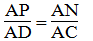
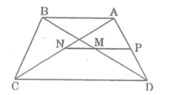
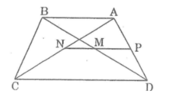
a. Gọi P là trung điểm của AD, nối PM
Trong ΔDAB ta có:
Suy ra:
Suy ra: PM // AB (Định lí đảo của định lí Ta-lét) (1)
Trong ΔACD, ta có
Suy ra:
Suy ra: PN // CD (định lí đảo định lí Ta-lét) (2)
Từ (1) và (2) và theo tiên đề Ơ-clít suy ra P, M, N thẳng hàng.
Vậy MN // CD hay MN // AB.
b. Vì PM là đường trung bình của tam giác DAB nên:
PM = AB/2 (tính chất đường trung bình tam giác)
Vì PN là đường trung bình của tam giác ΔACD nên:
PN = CD/2 (tính chất đường trung hình tam giác)
Mà PN = PM + MN
Suy ra: MN = PN – PM = CD/2 - AB/2 = (CD-AB)/2