NV
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TM
1
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 12 2020
\(S=\dfrac{1}{2018!\left(2019-2018\right)!}+\dfrac{1}{2016!\left(2019-2016\right)!}+...+\dfrac{1}{2!\left(2019-2\right)!}+\dfrac{1}{0!\left(2019-0!\right)}\)
\(\Rightarrow2019!.S=\dfrac{2019!}{2018!\left(2019-2018\right)!}+\dfrac{2019!}{2016!\left(2019-2016\right)!}+...+\dfrac{2019!}{2!\left(2019-2\right)!}+\dfrac{2019!}{0!\left(2019-0\right)!}\)
\(=C_{2019}^{2018}+C_{2019}^{2016}+...+C_{2019}^2+C_{2019}^0\)
\(=\dfrac{1}{2}\left(C_{2019}^0+C_{2019}^1+...+C_{2019}^{2018}+C_{2019}^{2019}\right)\)
\(=\dfrac{1}{2}.2^{2019}=2^{2018}\)
\(\Rightarrow S=\dfrac{2^{2018}}{2019!}\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1 2021
\(\dfrac{1}{u_n-1}=\dfrac{1}{\dfrac{2^n-5^n}{2^n+5^n}-1}=\dfrac{2^n+5^n}{-2.5^n}=-\dfrac{1}{2}\left[\left(\dfrac{2}{5}\right)^n+1\right]\)
\(\Rightarrow S_n=-\dfrac{1}{2}\left[\left(\dfrac{2}{5}\right)^1+\left(\dfrac{2}{5}\right)^2+...+\left(\dfrac{2}{5}\right)^n+n\right]\)
Lại có: \(\left(\dfrac{2}{5}\right)^1+\left(\dfrac{2}{5}\right)^2+...+\left(\dfrac{2}{5}\right)^n=\dfrac{2}{5}.\dfrac{1-\left(\dfrac{2}{5}\right)^n}{1-\dfrac{2}{5}}=\dfrac{2}{3}\left[1-\left(\dfrac{2}{5}\right)^n\right]\)
\(\Rightarrow S_n=-\dfrac{1}{2}\left[\dfrac{2}{3}-\dfrac{2}{3}\left(\dfrac{2}{5}\right)^n+n\right]=...\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 12 2021
\(u_n-4u_{n-1}+3u_{n-2}=5.2^n\)
\(\Leftrightarrow u_n-u_{n-1}-3\left(u_{n-1}-u_{n-2}\right)=5.2^n\)
Đặt \(u_n-u_{n-1}=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_1-u_0=4\\v_n-3v_{n-1}=5.2^n\end{matrix}\right.\)
\(\Rightarrow v_n+10.2^n=3\left(v_{n-1}+10.2^{n-1}\right)\)
Đặt \(v_n+10.2^n=x_n\Rightarrow\left\{{}\begin{matrix}x_1=v_1+10.2^1=24\\x_n=3x_{n-1}\end{matrix}\right.\)
\(\Rightarrow x_n\) là CSN với công bội 3
\(\Rightarrow x_n=24.3^{n-1}\)
\(\Rightarrow v_n=x_n-10.2^n=24.3^{n-1}-10.2^n=8.3^n-10.2^n\)
\(\Rightarrow u_n-u_{n-1}=8.3^n-10.2^n\)
\(\Rightarrow u_n-12.3^n+20.2^n=u_{n-1}-12.3^{n-1}+20.2^{n-1}\)
Đặt \(u_n-12.3^n+20.2^n=y_n\Rightarrow\left\{{}\begin{matrix}y_1=u_1-12.3^1+20.2^1=7\\y_n=y_{n-1}=...=y_1=7\end{matrix}\right.\)
\(\Rightarrow u_n=12.3^n-20.2^n+7\)
CM
21 tháng 11 2019
Xét số hạng tổng quát.
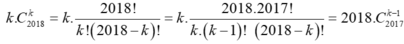
Cho k chạy từ 1 đến 2018 ta được:
Cho x=1 suy ra 
Chọn A.
27 tháng 11 2023
Đặt \(\dfrac{u_n}{n+1}=v_n\)
\(GT\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{u_1}{1+1}=1\\v_{n+1}=\dfrac{1}{4}v_n,\forall n\in N\text{*}\end{matrix}\right.\)
\(\Rightarrow v_n=\dfrac{1}{4}^{n-1},\forall n\in N\text{*}\)
\(\Rightarrow u_n=\left(n+1\right).\dfrac{1}{4}^{n-1},\forall n\in N\text{*}\)
21 tháng 8 2023
u1=-1
u2=-1+3=2
u3=2+3=5
u4=5+3=8
u5=8+3=11
Công thức tổng quát là: \(U_n=U_1+\left(n-1\right)\cdot\left(3\right)=-1+3n-3=3n-4\)
số số hạng là :
\(\left(2018-1\right):1+1=2018\)
tổng trên bằng
\(\left(\frac{1}{2018}+\frac{1}{2}\right).2018:2\)
\(=\frac{1010}{2018}.2018:2\)
\(=1010:2=505\)
P/s : ko chắc >: hình như sai
Công thức tính tổng
{(Số đầu + số cuối). số số hạng } :2