NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
N
1
TT
10 tháng 12 2020
Kẻ AH ⊥ DC tại H ; BK ⊥ DC tại K.
=> AH // BK
Xét t/g AHD vuông tại H và t/g BKC vuông tại K có:
AD = BC (do ABCD là htc)
\(\widehat{D}=\widehat{C}\)(do ABCD là htc)
=> t/g AHD = t/g BKC (ch-gn)
=> HD = KC ; AH = KB
Mà AH // BK
=> AHKB là hình thang
Lại có \(\widehat{AHK}=90^o\)
=> AHKB là hình chữ nhật
=> HK = AB = 10cm
Có
DH+HK+KC = DC
=> 2CK + 10 = 16 (cm)
=> CK = 3 (cm) Áp dụng đ/l Pythagoras vào t/g BKC vuông tại K có
\(BK^2+CK^2=BC^2\)
=> \(BK^2+3^2=5^2\)
=> BK = 4 (cm)
Có
\(S_{ABCD}=\dfrac{1}{2}.BK.\left(AB+CD\right)\)
\(=\dfrac{1}{2}.4.\left(10+16\right)=2.26=52\)cm2
Không chắc lắm :((
22 tháng 1 2021
Vẽ AE // BD, AH vg góc DC
=> ABDE là hbh(dhnb)
=> ED=AB=5cm, AE=BD=12cm
EC=ED+DC=5=15=20cm
Xét tg AEC có :
AE2+AC2=122+162= 400
EC2=202=400
=>AE2+AC2=EC2
=> tg AEC vg tại A
=> AH.EC=AE.AC
=>AH = 48/5 cm
S ht ABCD= ((5+12).48/5 ):2 = 96 cm2
HV
0
GV
Giáo viên Toán
Giáo viên
29 tháng 4 2017
a) \(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{10+6}{2}.5=40\left(cm^2\right)\)
b) Xem hình vẽ
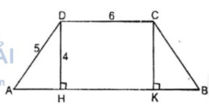
Tam giác vuông EAD có: \(AE=\sqrt{AD^2-DE^2}=\sqrt{5^2-4^2}=3\)
Vì ABCD là hình thang cân nên AE = FB = 3.
Suy ra AB = EF + AE + FB = 6 + 3 + 3 = 12.
\(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{12+6}{2}.4=36\left(cm^2\right)\)
TT
0
CM
29 tháng 4 2019
Áp dụng công thức tính diện tích hình thang.
S = (a+b)/2.h = (10+6)/2. 5 = 40( c m 2 )
ND
1
24 tháng 2 2017
Chung minh ABD đồng dạng với BDC
=> \(\widehat{ABD}\)=\(\widehat{BDC}\)
hai góc này ở vị trí sole trong
=> AB//CD
Kẻ 2 đường cao AH và BK
=> AHKB là hcn => AB = HK = 10cm
=> DH = KC = (16 - 10) : 2 = 3cm
Áp dụng Pytago trong tam giác vuông ADH ta đc:
AD2 = AH2 + DH2
=> AH = \(\sqrt{5^2-3^2}=4\)cm
Vậy SABCD = \(\frac{\left(10+16\right).4}{2}=52\) (cm2)