Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\left(x-2\right)^3+\left(5-2x\right)^3=0\)
\(\Leftrightarrow\left(x-2+5-2x\right)\left[\left(x-2\right)^2-\left(x-2\right)\left(5-2x\right)+\left(5-2x\right)^2\right]=0\)
\(\Leftrightarrow3-x=0\)
hay x=3

\(\left(x^2+2x\right)^2-2x^2-4x-3=0\Leftrightarrow x^4+4x^3+4x^2-2x^2-4x-3=0\Leftrightarrow x^4+4x^3+2x^2-4x-3=0\Leftrightarrow\left(x-1\right)\left(x+1\right)^2\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=3\end{matrix}\right.\)
Ta có: \(\left(x^2+2x\right)^2-2x^2-4x-3=0\)
\(\Leftrightarrow\left(x^2+2x\right)^2-2\left(x^2+2x\right)-3=0\)
\(\Leftrightarrow\left(x^2+2x-3\right)\left(x^2+2x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2\cdot\left(x+3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-3\\x=1\end{matrix}\right.\)

Ta có: \(2x^3+3x^2+2x+3=0\)
\(\Leftrightarrow x^2\left(2x+3\right)+\left(2x+3\right)=0\)
\(\Leftrightarrow2x+3=0\)
hay \(x=-\dfrac{3}{2}\)

a: Ta có: \(2-x=2\left(x-2\right)^3\)
\(\Leftrightarrow2\left(x-2\right)^3+x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left[2\left(x-2\right)^2+1\right]=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
c: Ta có: \(\left(x-1.5\right)^6+2\left(1.5-x\right)^3=0\)
\(\Leftrightarrow\left(x-1.5\right)^6-2\left(x-1.5\right)^3=0\)
\(\Leftrightarrow\left(x-1.5\right)^3\cdot\left[\left(x-1.5\right)^3-2\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1.5\\x=\sqrt[3]{2}+1.5\end{matrix}\right.\)

e) Ta có: \(x^3-4x-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2\right)-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2-14\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=12\end{matrix}\right.\)
e)x3-4x+14x(x-2)=0
⇔ x(x2-4)+14x(x-2)=0
⇔ x(x-2)(x+2)+14x(x-2)=0
⇔ (x-2)(x2+2x+14x)=0
⇔ x(x-2)(x+16)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-2=0\\x+16=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=2\\x=-16\end{matrix}\right.\)
g)x2(x+1)-x(x+1)+x(x-1)=0
⇔ (x+1)(x2-x)+x(x-1)=0
⇔ x(x+1)(x-1)+x(x-1)=0
⇔ x(x-1)(x+2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=1\\x=-2\end{matrix}\right.\)

a) \(x^3+3x^2+3x=0\Rightarrow x\left(x^2+3x+3\right)=0\Rightarrow x\left[\left(x+\dfrac{3}{2}\right)^2+\dfrac{3}{4}\right]=0\Rightarrow x=0\)
(do \(\left(x+\dfrac{3}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\))
b) \(x^3+6x^2+12x=0\Rightarrow x\left(x^2+6x+12\right)=0\Rightarrow x\left[\left(x+3\right)^2+4\right]=0\Rightarrow x=0\)
(do (x+3)2+4≥4>0)
a: Ta có: \(x^3+3x^2+3x=0\)
\(\Leftrightarrow x\left(x^2+3x+3\right)=0\)
hay x=0
b: Ta có: \(x^3+6x^2+12x=0\)
\(\Leftrightarrow x\left(x^2+6x+12\right)=0\)
hay x=0

x^2 - 2x - 15
= x^2 + 3x - 5x - 15
= x(x + 3) - 5(x + 3)
= (x - 5)(x + 3)
\(x^2-2x-15\)\(=\left(x^2-5x\right)+\left(3x-15\right)\)
\(=x\left(x-5\right)+3\left(x-5\right)=\left(x-5\right)\left(x+3\right)\)

a: \(M=m^2\left(m+n\right)-n^2m-n^3\)
\(=m^2\left(m+n\right)-n^2\left(m+n\right)\)
\(=\left(m+n\right)^2\left(m-n\right)\)
\(=\left(-2017+2017\right)^2\cdot\left(-2017-2017\right)\)
=0
b: \(N=n^3-3n^2-n\left(3-n\right)\)
\(=n^2\left(n-3\right)+n\left(n-3\right)\)
\(=n\left(n-3\right)\left(n+1\right)\)
\(=13\cdot10\cdot14=1820\)
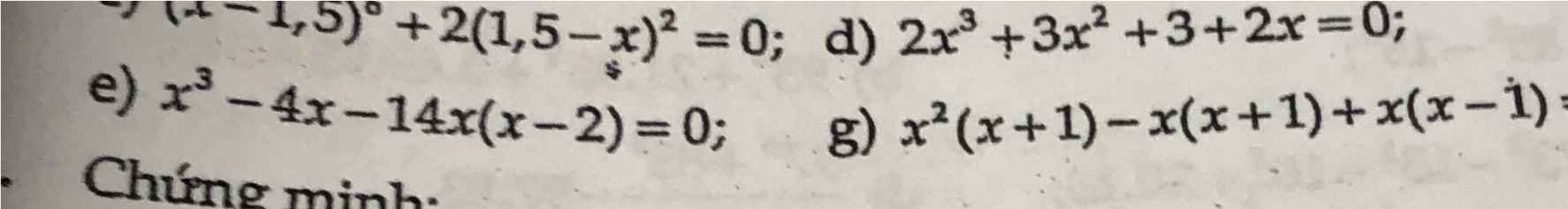
Bn ơi bn có thể giải thích câu đầu tiên đoạn sau giấu <=> đc ko?