Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


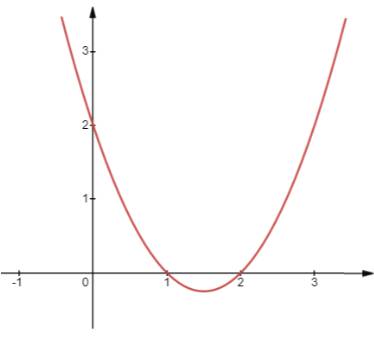
a) Đồ thị \(y = {x^2} - 3x + 2\)
- Có đỉnh là điểm \(I\left( {\frac{3}{2}; - \frac{1}{4}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{3}{2}\)
- \(a = 1 > 0\), quay bề lõm lên trên
- Đi qua điểm (0;2);(1;0)
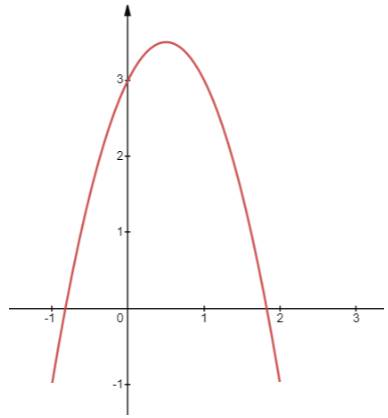
b) Đồ thị \(y = - 2{x^2} + 2x + 3\)
- Có đỉnh là điểm \(I\left( {\frac{1}{2};\frac{7}{2}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{1}{2}\)
- \(a = - 2 < 0\), quay bề lõm xuống dưới
- Đi qua điểm (0;3);(1;3)
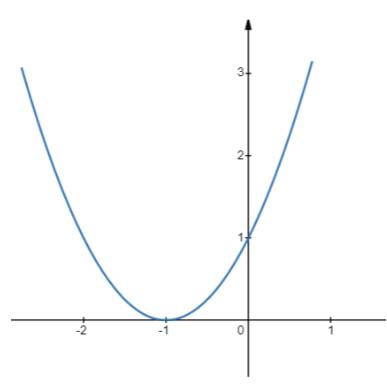
c) Đồ thị\(y = {x^2} + 2x + 1\)
- Có đỉnh là điểm \(I( - 1;0)\), có trục đối xứng là đường thẳng \(x = - 1\)
- \(a = 1 > 0\), quay bề lõm lên trên
- Đi qua điểm (0;1); (1;4)
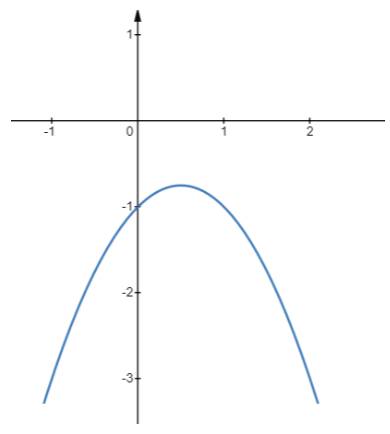
d) Đồ thị \(y = - {x^2} + x - 1\)
- Có đỉnh là điểm \(I\left( {\frac{1}{2};\frac{{ - 3}}{4}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{1}{2}\)
- \(a = - 1 < 0\), quay bề lõm xuống dưới
- Đi qua điểm (0;-1); (1;-1)

Ta có TXĐ:D=R
⇒∀x∈D⇒−x∈D
Đồ thị hàm số đã cho nhận gốc tọa độ O làm tâm đối xứng khi và chỉ khi nó là hàm số lẻ
⇔f(−x)=−f(x),∀x∈R
\(\text{⇔(−x)^3−(m^2−9)(−x)^2+(m+3)(−x)+m−3}\)
\(\text{=-[x^3−(m^2−9)x^2+(m+3)x+m−3]}\)
\(=\text{⇔2(m^2−9)x^2−2(m−3)=0}\)
\(\Rightarrow\forall\inℝ\) ;
\(\hept{\begin{cases}m^2-9=0\\m-3=0\end{cases}}\)
\(\hept{\begin{cases}m=\pm3\\m=3\end{cases}}\)
\(\Rightarrow m=3\)

a) y xác định \(\Leftrightarrow2x^2-5x+2\ne0\Leftrightarrow\left(x-2\right)\left(2x-1\right)\ne0\Leftrightarrow\left\{{}\begin{matrix}x-2\ne0\\2x-1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne2\\x\ne\frac{1}{2}\end{matrix}\right.\). Vậy tập xác định D = R / { 2; 1/2}
b) y xác định \(\Leftrightarrow\left\{{}\begin{matrix}x-1\ne0\\2x+4\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ge-2\end{matrix}\right.\).
Vậy tập xác định D = \([-2;+\infty)/1\)
y xác định \(\Leftrightarrow x^2-3x+m-1\ne0\forall x\in R\)
suy ra phương trình x2 - 3x + m - 1 = 0 vô nghiệm
\(\Rightarrow\Delta=9-4\left(m-1\right)< 0\Leftrightarrow9-4m+4< 0\Leftrightarrow m>\frac{13}{4}\)
\(\Rightarrow m\in\left(\frac{13}{4};+\infty\right)\)

a: ĐKXĐ: \(\left(2x^2-5x+2\right)\left(x^3+1\right)< >0\)
=>(2x-1)(x-2)(x+1)<>0
hay \(x\notin\left\{\dfrac{1}{2};2;-1\right\}\)
b: ĐKXĐ: x+5<>0
=>x<>-5
c: ĐKXĐ: x4-1<>0
hay \(x\notin\left\{1;-1\right\}\)
d: ĐKXĐ: \(x^4+2x^2-3< >0\)
=>\(x\notin\left\{1;-1\right\}\)