
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NB
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên
FH
1

15 tháng 11 2021
Ta có: (x3 +
)8=Ck8 x3(8 – k) ()k =Ck8 x24 – 4k
Trong tổng này, số hạng Ck8 x24 – 4k không chứa x khi và chỉ khi

28 tháng 9 2021
Trả lời :
Có 520 số chẵn gồm bốn chữ số đôi một khác nhau được lập từ các số 0,1,2,4,5,6,7.
# Hok tốt !

2 tháng 10 2021
(m+2)sinx+mcosx=2(m+2)sinx+mcosx=2
Phương trình có nghiệm
⇔(m+2)2+m2≥22⇔2m2+4m+4≥4⇔m2+2m≥0⇔[m≥0m≤−2⇔(m+2)2+m2≥22⇔2m2+4m+4≥4⇔m2+2m≥0⇔[m≥0m≤−2
b) Phương trình (2m−1)sinx+(m−1)cosx=m−3(2m−1)sinx+(m−1)cosx=m−3 vô nghiệm
⇔(2m−1)2+(m−1)2≤(m−3)2⇔4m2−4m+1+m2−2m+1≤m2−6m+9⇔4m2≤7⇔m2≤74⇔−√72≤m≤√72

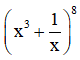

giúp mk với !!!