Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{15}{17}-0,3+\left(-\frac{22}{16}\right)+\frac{3}{10}-1\frac{4}{9}\)

a,\(\left(\dfrac{-2}{3}+\dfrac{3}{7}\right):\dfrac{4}{5}+\left(\dfrac{-1}{3}+\dfrac{4}{7}\right):\dfrac{4}{5}\)
\(=\left(-\dfrac{2}{3}+\dfrac{3}{7}\right).\dfrac{5}{4}+\left(\dfrac{-1}{3}+\dfrac{4}{7}\right).\dfrac{5}{4}\)
\(=\left(\dfrac{-2}{3}+\dfrac{3}{7}+\dfrac{-1}{3}+\dfrac{4}{7}\right).\dfrac{5}{4}\)
\(=\left(-1+1\right).\dfrac{5}{4}=0\)
Chúc bạn học tốt!!!
Câu b làm tương tự!
a) Đoàn Đức Hiếu
b) \(\dfrac{5}{9}:\left(\dfrac{1}{11}-\dfrac{5}{22}\right)+\dfrac{5}{9}:\left(\dfrac{1}{15}-\dfrac{2}{3}\right)\)
\(=\dfrac{5}{9}:\left(-\dfrac{3}{22}\right)+\dfrac{5}{9}:\left(-\dfrac{3}{5}\right)\)
\(=-\dfrac{5}{9}\cdot\dfrac{22}{3}-\dfrac{5}{9}\cdot\dfrac{5}{3}\)
\(=-\dfrac{110}{27}-\dfrac{25}{27}\)
\(=-5\)

\(\left(\frac{3}{4}x-\frac{9}{16}\right)-\left(\frac{1}{3}+\frac{-3}{5}x\right)=0.\)
\(\frac{3}{4}x-\frac{9}{16}-\frac{1}{3}-\frac{-3}{5}x=0\)
\(\frac{27}{20}x-\frac{43}{48}=0\)
\(\frac{27}{20}x=\frac{43}{48}\)
\(x=\frac{215}{324}\)
mong ủng hộ mk
(3 phần 4 nhân X - 9 phần 16 ) - (1 phần 3 + -3 phần 5 chia X ) = 0
=>\(\frac{3}{4}.x-\frac{9}{16}=\frac{1}{3}+\frac{-3}{5}:x\)
=\(\frac{3}{4}.x-\frac{9}{16}=\frac{-4}{15}:x\)
=>\(\frac{3}{4}.x-\frac{-4}{15}:x=\frac{9}{16}\)
Đến đây thì mk chịu =)
Dù sao thi cg ti.ck giúp mk tí

Bài 1:
a: \(2P=2^{101}-2^{100}+2^{98}-2^{97}+...+2^3-2^2\)
=>\(3P=2^{101}-2\)
hay \(P=\dfrac{2^{101}-2}{3}\)
b: \(5Q=5^{101}-5^{100}+5^{99}-5^{98}+...+5^3-5^2+5\)
=>\(6Q=5^{101}+1\)
hay \(Q=\dfrac{5^{101}+1}{6}\)
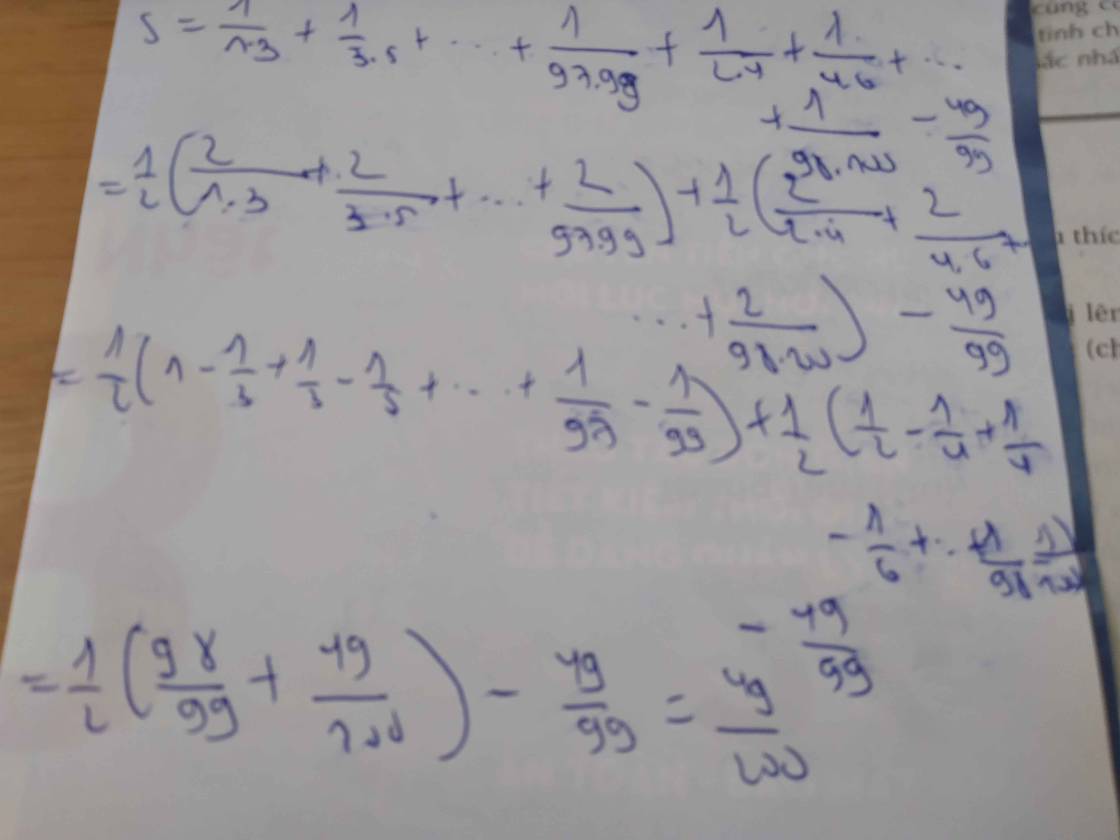
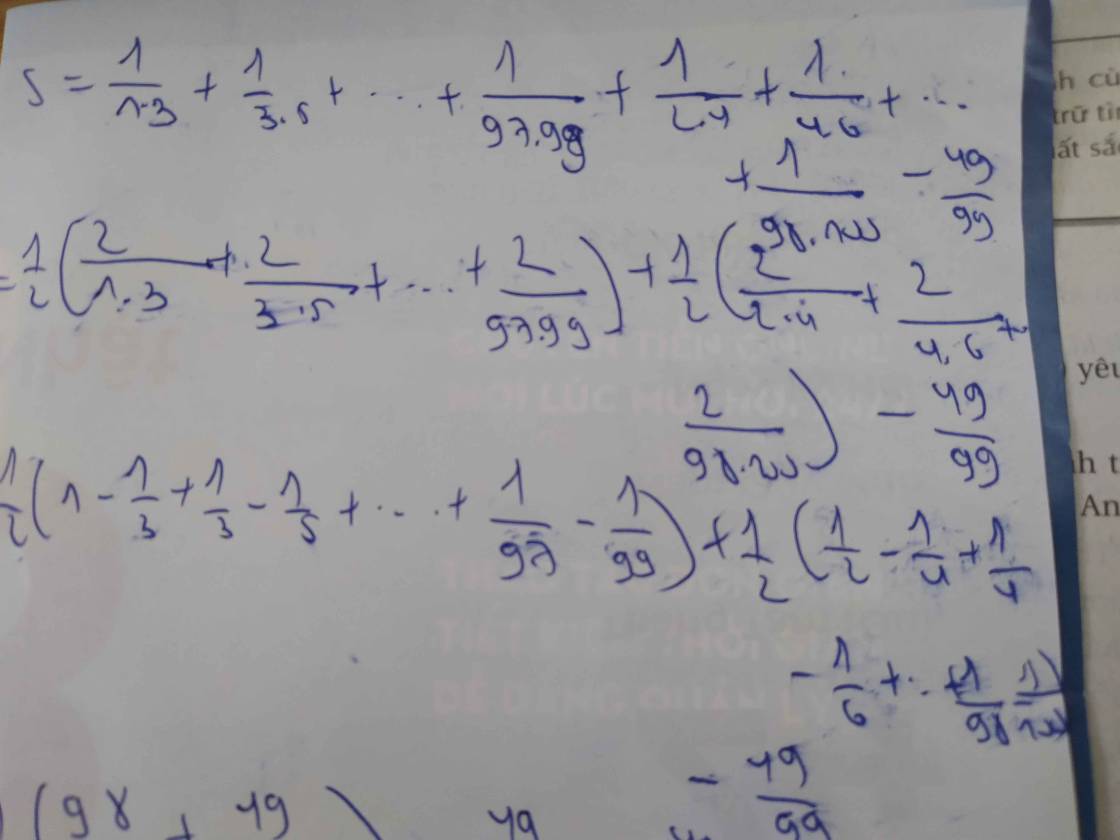

Làm lại đề cho:
\(\left(\frac{1}{4}-1\right)\cdot\left(\frac{1}{9}-1\right)\cdot\left(\frac{1}{16}-1\right)...\left(\frac{1}{81}-1\right)\cdot\left(\frac{1}{100}-1\right)\)
Tính nhẩm
TOI KO BIET