Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hệ vật "lò xo - vật - Trái Đất" là hệ cô lập (do không chịu ngoại lực tác dụng) nên cơ năng của hệ vật bảo toàn.
Chọn mặt phẳng ngang đi qua vị trí A làm mốc tính thế năng trọng trường ( W t = 0) và chọn vị trí lò xo không bị biến dạng làm mốc thế năng đàn hồi ( W đ h = 0). Khi đó cơ năng của hệ vật tại vị trí bất kì có giá trị bằng tổng của động năng W đ thế năng trọng trường W t và thế năng đàn hồi W đ h :
W = W đ + W t + W đ h = m v 2 /2 + mgh + k ∆ l 2 /2
ại vị trí A, lò xo bị nén một đoạn ∆ l = (10 + 30). 10 - 2 = 40. 10 - 2 m, vật có động năng W đ (A) = 0 và thế năng trọng trường W t (A) = 0, nên cơ năng của hệ vật tại A đúng bằng thế năng đàn hồi của lò xo :
W(A) = W đ h (A) = k ∆ l 2 /2 = 800. 40 . 10 - 2 2 = 64(J)
Khi buông nhẹ tay để thả cho vật từ vị trí A chuyển động lên phía trên tới vị trí B cách A một đoạn ∆ l = 40 cm, tại đó lò xo không bị biến dạng, thế năng đàn hồi W đ h = 0. Sau đó, vật tiếp tục chuyển động từ vị trí B lên tới vị
trí C có độ cao h m a x = BC, tại đó vật có vận tốc v C = 0 và động năng W đ (C) = 0, nên cơ năng của hệ vật tại C bằng :
W(C) = mg( ∆ l + h m a x ) + k h m a x 2 /2
Áp dụng định luật bảo toàn cơ năng cho chuyển động của hệ vật từ vị trí A qua vị trí B tới vị trí C, ta có :
W(C) = W(B) = W(A) ⇒ mg( ∆ l + h m a x ) + k h m a x 2 /2 = 64
Thay số, ta tìm được độ cao h m a x = BC :
8.10.(40. 10 - 2 + h m a x ) + 800. h m a x /2 = 64 ⇒ 50 h 2 + 10h - 4 = 0
Phương trình này có nghiệm số dương : h m a x = BC = 20 cm.
Như vậy, độ cao lớn nhất mà vật đạt tới so với vị trí A bằng :
H m a x = AB + BC = 40 + 20 = 60 cm

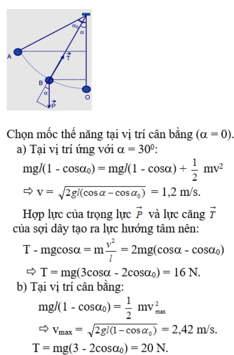
a) \(h=l-l\cos\alpha_0=1m\)
\(W=W_d+W_t=mgh=1J\)
b) Tính lực căng của dây treo khi vật qua vị trí cân bằng
Hai lực tác dụng vào vật: \(\overrightarrow{P},\overrightarrow{T}\)
Hợp lực: \(\overrightarrow{F}=\overrightarrow{P}+\overrightarrow{T}=m.\overrightarrow{a_{ht}}\)
\(m\frac{v^2_0}{l}=-P+T\)
\(T=m\frac{v^2_0}{l}+mg\)
\(T=3mg-2mg\cos\alpha_0=2N\)

Đáp án B
Giai đoạn 1:
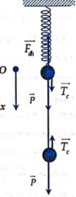
- Sau khi kéo vật B xuống dưới 20 cm và thả nhẹ thì hệ đi lên, hai vật A và B cùng vận tốc, gia tốc đến khi lực căng dây bằng 0.
![]()
Giai đoạn 2:
- Dây chùng vật B chuyển động giống như vật được ném thẳng đứng lên trên với vận tốc ban đầu ở giai đoạn này là vận tốc ở cuối giai đoạn (Tc = 0)
- Vận tốc đầu giai đoạn 2 tính từ định luật bảo toàn cơ năng cho con lắc là:
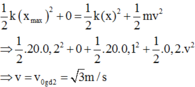
- Quãng đường đi được ở giai đoạn 2 đến khi dừng lại (đạt độ cao lớn nhất) là:
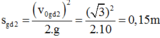
- Kết thúc giai đoạn 2 vật B đã lên đến độ cao so với ban đầu khi buông là:
![]()
Giai đoạn 3:
Vật B tuột khỏi dây từ độ cao 4,5m rơi đến vị trí thả ban đầu là chuyển động rơi tự do, ta có:
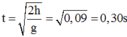

Thế năng đàn hồi:
\(W_{đh}=\dfrac{1}{2}k\cdot\left(\Delta x\right)^2=\dfrac{1}{2}\cdot k\cdot0,12^2=7,2\cdot10^{-3}k\left(J\right)\)
Cơ năng tại vị trí cân bằng của quả cầu:
\(W=\dfrac{1}{2}mv^2+mgz\left(J\right)\)
Bảo toàn cơ năng: \(W_{đh}=W\)
\(\Rightarrow7,2\cdot10^{-3}k=\dfrac{1}{2}mv^2+mgz\)
\(\Rightarrow0,0144k=mv^2+2mgz\)
\(\Rightarrow z=\dfrac{0,0144k-mv^2}{2mg}\)
Nếu có số liệu cụ thể thì bạn tự thay vào nha

Chọn trục tọa độ Oy hướng tâm như hình vẽ
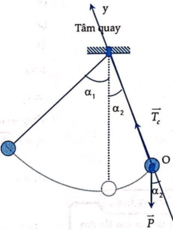
Phương trình định luật II Niu - tơn cho vật là
Chiếu lên phưong hướng tâm Oy ta được
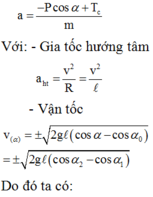
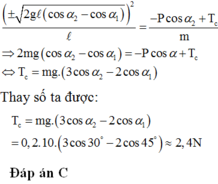

a) Thế năng trọng trường tại vị trí ném: \(W_{t1}=mgh_1=2.10.10=200(J)\)
Động năng: \(W_{đ1}=\dfrac{1}{2}mv^2=\dfrac{1}{2}.2.20^2==400(J)\)
Ở độ cao cực đại thì thế năng bằng cơ năng \(\Rightarrow W_{t2}=W=W_{đ1}+W_{t1}=400+200=600(J)\)
Lúc chạm đất, h = 0 \(\Rightarrow W_t=0\)
Sau khi ném 1s, độ cao của vật đạt được: \(h=10+20.1-\dfrac{1}{2}.10.1^2=25m\)
Thế năng lúc này: \(W_{t3}=m.g.h=2.10.25=500(J)\)
b) Độ cao cực đại của vật: \(h_{max}=\dfrac{W}{mg}=\dfrac{600}{2.10}=30(m)\)
Công của trọng lực từ lúc ném đến khi thế năng cực đại là: \(A_1=-2.10.(30-10)=400(J)\)
Công của trọng lực từ lúc ném đến khi chạm đất: \(A_2=2.10.10=200(J)\)