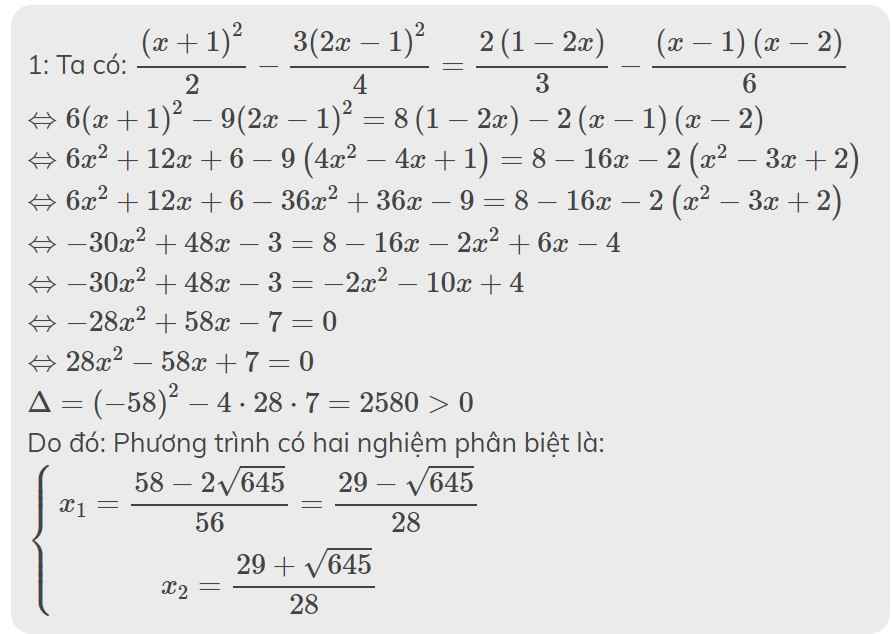Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Ta có: \(\dfrac{\left(x+1\right)^2}{2}-\dfrac{3\left(2x-1\right)^2}{4}=\dfrac{2\left(1-2x\right)}{3}-\dfrac{\left(x-1\right)\left(x-2\right)}{6}\)
\(\Leftrightarrow6\left(x+1\right)^2-9\left(2x-1\right)^2=8\left(1-2x\right)-2\left(x-1\right)\left(x-2\right)\)
\(\Leftrightarrow6x^2+12x+6-9\left(4x^2-4x+1\right)=8-16x-2\left(x^2-3x+2\right)\)
\(\Leftrightarrow6x^2+12x+6-36x^2+36x-9=8-16x-2\left(x^2-3x+2\right)\)
\(\Leftrightarrow-30x^2+48x-3=8-16x-2x^2+6x-4\)
\(\Leftrightarrow-30x^2+48x-3=-2x^2-10x+4\)
\(\Leftrightarrow-28x^2+58x-7=0\)
\(\Leftrightarrow28x^2-58x+7=0\)
\(\text{Δ}=\left(-58\right)^2-4\cdot28\cdot7=2580>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{58-2\sqrt{645}}{56}=\dfrac{29-\sqrt{645}}{28}\\x_2=\dfrac{29+\sqrt{645}}{28}\end{matrix}\right.\)

Gọi quãng đường AB là x (km)
Suy ra: Thời gian đi của An là \(\frac{x}{12}\)(giờ)
Thời gian về nửa đoạn đường đầu là \(\frac{0,5x}{10}\)(giờ)
Thới gian về nửa đoạn đường sau là \(\frac{0,5x}{8}\)(giờ)
Vận tốc trung bình của Nam cả đi lẫn về là \(\frac{x+0,5x+0,5x}{\frac{x}{12}+\frac{0,5x}{10}+\frac{0,5x}{8}}\)
Bạn tự tính nhé.

Tỉ số vận tốc đi với vận tốc về là
16:24 = 2/3
Vì cùng 1 quãng đường vận tôc và thời gian là 2 đại lượng tỉ lệ nghịch
Tỉ số thời gian đi với thời gian về là 3/2
Tổng số phần bằng nhau : 3 + 2 = 5 phần
=> Thời gian đi là 10 : 5 x 3 = 6 giờ
=> Thời gian về là 10 - 6 = 4 giờ
=> Quãng sông AB dài : 16 x 6 = 96 km