Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Không gian mẫu: Số cách chia 15 học sinh thành 5 nhóm, mỗi nhóm 3 học sinh:
n Ω = C 15 3 . C 12 3 . C 9 3 . C 6 3 . C 3 3 5 ! = 1401400.
Vì cả 5 nhóm đều có học sinh giỏi và khá nên sẽ có đúng 1 nhóm có 2 học sinh giỏi, 1 học
sinh khá, các nhóm còn lại đều có 1 giỏi, 1 khá và 1 trung bình.
Số kết quả thỏa mãn:
n P = C 6 2 . C 5 1 .4 ! .4 ! = 43200.
Xác suất cần tính:
n P n Ω = 216 7007 .

Chọn C.
Số phần tử của không gian mẫu là n ( Ω ) = C 9 3 . C 6 3 . C 3 3 .
Gọi X là biến cố “nhóm nào cũng có học sinh giỏi và học sinh khá”
Khi đó, ta xét các chia nhóm như sau:
· N1: 2 học sinh giỏi, 1 học sinh khá.
· N2: 1 học sinh giỏi, 1 học sinh khá và
· 1 học sinh trung bình.
· N3: 1 học sing giỏi, 1 học sinh khá
· và 1 học sinh trung bình.
Suy ra có 3 . ( C 4 2 . C 3 1 ) . C 2 1 . C 2 1 . C 2 1 cách chia ⇒ n ( X ) = 3 . C 4 2 . C 3 1 . C 2 1 . C 2 1 . C 2 1 .
Vậy xác suất cần tính là P = n ( X ) n ( Ω ) = 9 35

Vì các học sinh lớp 10A1 đều học giỏi ít nhất một trong hai môn Toán hoặc Tiếng Anh nên số học sinh của lớp là: 30 + 25 - 16 = 39 (học sinh).
Chọn C.
Vì các học sinh lớp 10A1 đều học giỏi ít nhất một trong hai môn Toán hoặc Tiếng Anh nên số học sinh của lớp là: 30 + 25 - 16 = 39 (học sinh).

Số học sinh xếp loại giỏi là:
40 . 40%=16(học sinh)
Số học sinh khá lớp 6A là:
16 . 5/4=20(học sinh)
Số học sinh TB lớp 6A là:
40-16-20=4(học sinh)
Đáp số : 4 học sinh
Chúc bạn học tốt!

Tỉ số của học sinh giỏi và khá đối với cả lớp là:
1 - 7/15 = 8/15 (số học sinh cả lớp)
Tỉ số của số học sinh giỏi và số học sinh còn lại là:
1 - 5/8 = 3/8 (số học sinh còn lại)
Tỉ số của học sinh giỏi và học sinh cả lớp là:
3/8 x 8/15 = 1/5 (số học sinh cả lớp)
Số học sinh của cả lớp là:
9 : 1/5 = 45 (học sinh)
Số học sinh trung bình là:
45 x 7/15 = 21 (học sinh)
Số học sinh khá là:
45 - 21 - 9 = 15 (học sinh)
Đáp số: ...........


Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
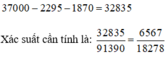
Chọn D