Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

minh giai phan d, nha bn :
x-a/b+c + x-b/c+a + x-c/a+b=3
=> (x-a/b+c - 1)+(x-b/a+c - 1 )+(x-c/a+b - 1) = 3-3=0
=>x-a-b-c/b+c + x-a-b-c/a+c + x-a-b-c/a+b =0
=>(x-a-b-c)(1/b+c + 1/a+c + 1/a+b )=0
Vi 1/b+c + 1/a+c + 1/a+b luon lon hon 0=>x-a-b-c=0
=>x=a+b+c

1: \(\Leftrightarrow\left(x+2\right)\left(x-2\right)+3\left(x+1\right)=3+x^2-x-2\)
\(\Leftrightarrow x^2-x+1=x^2-4+3x+3=x^2+3x-1\)
=>-4x=-2
hay x=1/2
2: \(\Leftrightarrow\left(x+6\right)^2+\left(x-5\right)^2=2x^2+23x+61\)
\(\Leftrightarrow x^2+12x+36+x^2-10x+25=2x^2+23x+61\)
\(\Leftrightarrow2x^2+23x+61=2x^2+2x+11\)
=>21x=-50
hay x=-50/21
3: \(\Leftrightarrow6\left(x-8\right)+\left(x+2\right)\left(x-5\right)=-18-\left(x-5\right)\left(x-8\right)\)
\(\Leftrightarrow6x-48+x^2-3x-10+18+x^2-13x+40=0\)
\(\Leftrightarrow2x^2-10x=0\)
=>2x(x-5)=0
=>x=0(nhận) hoặc x=5(loại)

Nguyễn TrươngNguyễn Việt LâmNguyenTruong Viet TruongKhôi BùiAkai HarumaÁnh LêDƯƠNG PHAN KHÁNH DƯƠNGPhùng Tuệ Minhsaint suppapong udomkaewkanjana

a) ĐKXĐ: x # 1
Khử mẫu ta được: 2x - 1 + x - 1 = 1 ⇔ 3x = 3 ⇔ x = 1 không thoả mãn ĐKXĐ
Vậy phương trình vô nghiệm.
b) ĐKXĐ: x # -1
Khử mẫu ta được: 5x + 2x + 2 = -12
⇔ 7x = -14
⇔ x = -2
Vậy phương trình có nghiệm x = -2.
c) ĐKXĐ: x # 0.
Khử mẫu ta được: x3 + x = x4 + 1
⇔ x4 - x3 -x + 1 = 0
⇔ x3(x – 1) –(x – 1) = 0
⇔ (x3 -1)(x - 1) = 0
⇔ x3 -1 = 0 hoặc x - 1 = 0
1) x - 1 = 0 ⇔ x = 1
2) x3 -1 = 0 ⇔ (x - 1)(x2 + x + 1) = 0
⇔ x = 1 hoặc x2 + x + 1 = 0 ⇔ \(\left(x+\dfrac{1}{2}\right)^2=-\dfrac{3}{4}\) (vô lí)
Vậy phương trình có nghiệm duy nhất x = 1.
d) ĐKXĐ: x # 0 -1.
Khử mẫu ta được x(x + 3) + (x + 1)(x - 2) = 2x(x + 1)
⇔ x2 + 3x + x2 – 2x + x – 2 = 2x2 + 2x
⇔ 2x2 + 2x - 2 = 2x2 + 2x
⇔ 0x = 2
Phương trình 0x = 2 vô nghiệm.
Vậy phương trình đã cho vô nghiệm

a: \(=\dfrac{4a^2-4a+1-4a^2-2a+6a+3}{\left(2a-1\right)\left(2a+1\right)}\)
\(=\dfrac{4}{\left(2a-1\right)\left(2a+1\right)}\)
b: \(=\dfrac{x-1-x-1+2x^2}{\left(x-1\right)\left(x+1\right)}=2\)
d: \(=\dfrac{x-5+6x}{x\left(x+3\right)}=\dfrac{7x-5}{x\left(x+3\right)}\)
e: \(=\dfrac{x^2-4+3}{x-2}=\dfrac{x^2-1}{x-2}\)
i: \(=\dfrac{x}{x\left(x-4\right)}-\dfrac{3}{5x}=\dfrac{1}{x-4}-\dfrac{3}{5x}\)
\(=\dfrac{5x-3x+12}{5x\left(x-4\right)}=\dfrac{2x+12}{5x\left(x-4\right)}\)

a, \(\dfrac{x^2-x}{x-2}+\dfrac{4-3x}{x-2}\)
\(=\dfrac{x^2-x+4-3x}{x-2}=\dfrac{x^2-4x+4}{x-2}\)
c) \(\dfrac{2}{x^2-9}+\dfrac{1}{x+3}\)
Ta có: \(\dfrac{1}{x+3}=\dfrac{1\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{x-3}{x^2-9}\)
\(\Rightarrow\dfrac{2}{x^2-9}+\dfrac{1}{x+3}=\dfrac{2}{x^2-9}+\dfrac{x-3}{x^2-9}=\dfrac{2+x-3}{x^2-9}=\dfrac{x-1}{x^2-9}\)

\(\Leftrightarrow\dfrac{2x}{a^2-a+1}+\dfrac{-4x}{2a^2-2a+2a^2}+\dfrac{2ax}{1+a^3}< \dfrac{1}{2a+2}-\dfrac{1}{2a^2-2a+2}+\dfrac{a}{1+a^3}\)
\(\Leftrightarrow\left(\dfrac{2}{a^2-a+1}-\dfrac{4}{2a^2-2a+2}+\dfrac{2a}{1+a^3}\right).x< \left(\dfrac{1}{2a+2}-\dfrac{1}{2a^2-2a+2}+\dfrac{a}{1+a^3}\right)\)
\(\Leftrightarrow\left(\dfrac{2a}{1+a^3}\right)x< \dfrac{\left(a^2-a+1\right)-\left(a+1\right)+2a}{2.\left(a+1\right)\left(a^2-a+1\right)}=\dfrac{a^2}{1+a^3}\)
\(\Leftrightarrow\left(\dfrac{2a}{1+a^3}\right)x< \dfrac{a^2}{2.\left(1+a^3\right)}\)
\(a=0\Rightarrow vo...N_o\)
\(\left\{{}\begin{matrix}\dfrac{2a}{a^3+1}>0\Leftrightarrow\left[{}\begin{matrix}a< -1\\a>0\end{matrix}\right.\\x< \dfrac{a^2}{2\left(a^3+1\right)}:\dfrac{2a}{\left(a^3+1\right)}=\dfrac{a}{2}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\dfrac{2a}{a^3+1}< 0\Rightarrow-1< a< 0\\x>\dfrac{a}{2}\end{matrix}\right.\)
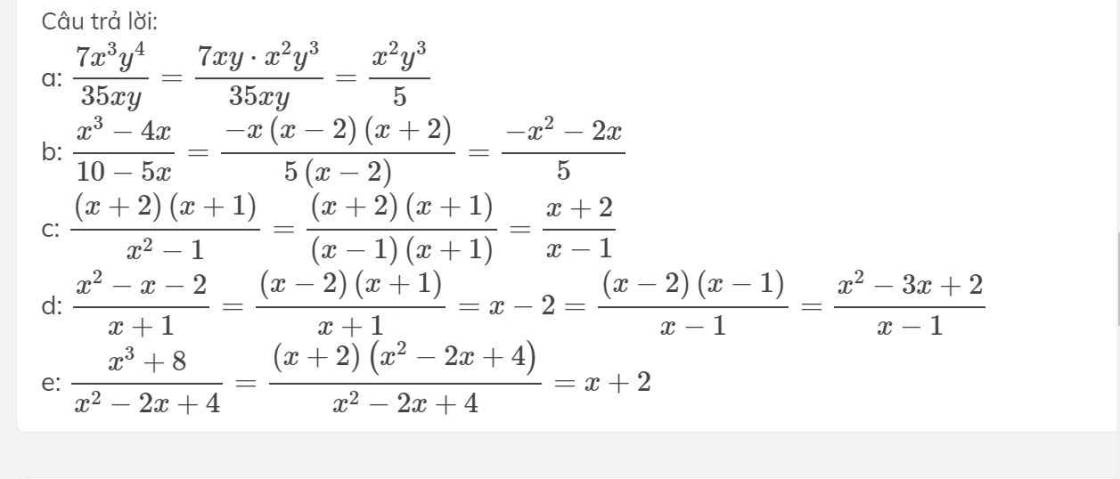
bài 2:
\(S=\dfrac{1}{1+x1+x1x2}+\dfrac{1}{1+x2+x2x3}+\dfrac{1}{1+x3+x3x1}\)
=\(S=\dfrac{1}{1+x1+x1x2}+\dfrac{x1}{x1\left(1+x2+x2x3\right)}+\dfrac{x1x2}{x2x1\left(1+x3+x3x1\right)}\)
S=\(\dfrac{1}{x+x1+x1x2}+\dfrac{x1}{x1+x1x2+1}+\dfrac{x1x2}{x1x2+1+x1}\)
S=\(\dfrac{1+x1+x1x2}{x1x2+1+x1}=1\)
chúc bạn học tốt ^^