
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Phương pháp: Sử dụng công thức tính chu kì dao động của con lắc lò xo dao động điều hoà
Cách giải:
Chu kỳ dao động của con lắc lò xo được tính bởi công thức: T = 2 π m k
Khi k tăng gấp đôi, m giảm 1 nửa thì chu kỳ T giảm đi 2 lần.


T=0.4s => denta l=4 cm
thời gian dãn gấp 2 lần thời gian nén nên tnen = T/3
nếu chọn chiều (+) hướng xuống thì vị trí mà lo xo dãn là từ 2pi/3 -> 4pi/3
nên A = 8 cm

Đáp án C
Lời giải chi tiết:
Chu kì của con lắc lò xo chỉ phụ thuộc vào độ cứng của lò xo và khối lượng của vật nặng.
Nếu giảm một nửa chiều dài của lò xo thì độ cứng tăng gấp đôi.
Đồng thời ta giảm một nữa khối lượng vật nặng, chu kì mới của lò xo.
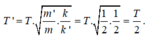

Ban đầu, ở VTCB, lò xo dãn: \(\Delta l_0=\frac{mg}{k}=\frac{1.10}{100}=0,1m=10cm\)
Do nâng vật lên cho lò xo có chiều dài tự nhiên rùi thả nhẹ, nên biên độ \(A=\Delta l_0=10cm\)
Khi vật xuống vị trí thấp nhât, được gắn thêm vật m0 thì ở VTCB lò xo dãn \(\Delta l_0'=15cm\)
Biên độ dao động mới lúc này: A'= 10 - 5 = 5cm (Do VTCB bị thấp xuống 5cm so với lúc đầu, mà vị trí biên không đổi nên biên độ giảm 5cm).
Ta có tỉ lệ cơ năng: \(\frac{W'}{W}=\frac{A'^2}{A^2}=\frac{1}{4}\)(do độ cứng lò xo không đổi)
Suy ra cơ năng sau giảm bằng 1/4.
Nên cơ năng giảm 3/4 cơ năng ban đầu = \(\frac{3}{4}.\frac{1}{2}.100.0,1^2=0,375J\)
Đáp án A.




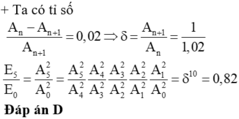
tần số dao động
\(\omega=\sqrt{\frac{k}{m}}\)
Chu kỳ dao động là
\(T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{k}}\)
suy ra
\(\frac{T_2}{T_1}=\sqrt{\frac{m_2}{m_1}}=\sqrt{\frac{47}{50}}\)
Chu kỳ giảm đi
\(\left(1-\sqrt{\frac{47}{50}}\right).100\%=3,05\%\)
thanks Sky SơnTùng