Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) tính BC:
Áp dụng định lí Py-tago vào \(\Delta\)vuông ABC
ta có: BC2=BA2+AC2
=>BC2= 62+82
=> BC2= 36+64
=>BC2= 100
=> BC= \(\sqrt{100}\)
=> BC= 10 (cm)
b)c/m \(\Delta\)HAB đồng dạng \(\Delta\)HCA:
Ta có: - tam giác HAB đồng dạng với tam giác ABC ( \(\widehat{B}\)chung)
- tam giác HAC đồng dạng với tam giác ABC ( \(\widehat{C}\)chung)
=> \(\Delta HAB\)đồng dạng \(\Delta HCA\)( cùng đồng dạng \(\Delta ABC\))
có bạn nào giúp minh câu c và d được k. mình k cho

tự vẽ hình nhé
a, Xét \(\Delta\) MNP và \(\Delta\) HNM
< MNP chung
<NMP=<NHM(=90\(^0\) )
b,=> \(\dfrac{MN}{HN}=\dfrac{NP}{MN}\)
=> \(MN^2=NP\cdot NH\)
c, xét \(\Delta\) NMP vg tại M, áp dụng định lí Py - ta - go trong tam giác vg có
\(MN^2+MP^2=NP^2\)
=> \(NP^2=144\Rightarrow NP=12cm\)
Ta có \(MN^2=NH\cdot NP\)
Thay số:\(7,2^2=NH\cdot12\Rightarrow NH=4,32cm\)
N P M K Q 1
a) ∆MNP là tam giác vuông, nên theo định lý Pytago ta có:
NP2=MN2+MP2=>NP=\(\sqrt{MN^2+MP^2}\)=\(\sqrt{8^2+6^2}\)=10(cm)
Ta có: MK là đường phân giác của ∆MNP =>\(\dfrac{NK}{KP}\) =\(\dfrac{MN}{MP}\) =\(\dfrac{4}{3}\)
=> \(\dfrac{NK}{4}\)=\(\dfrac{KP}{3}\)
Theo tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{NK}{4}\)=\(\dfrac{KP}{3}\)=\(\dfrac{NK+KP}{4+3}\)=\(\dfrac{10}{7}\)=> NK=5,71(cm); KP=4,29(cm)
b)Ta có: +
+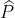 =90°;
=90°; 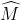 1+
1+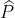 =90°=>
=90°=>  =
=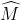 1
1
∆NQM đồng dạng ∆MQP
góc N =góc M1
góc Q: chung
=> \(\dfrac{NQ}{QM}\)=\(\dfrac{MQ}{QP}\)=>
MQ2=NQ.QP
c) SMNP=\(\dfrac{1}{2}\).MN.MP=\(\dfrac{1}{2}\).8.6=24(cm2)
=\(\dfrac{1}{2}\).MQ.NP=\(\dfrac{1}{2}\).MQ.10=24=>MQ=4,8(cm2)
Tam giác NMQ đồng dạng tam giác NPM
Góc Q= góc M (=90 độ)
Góc N: chung
=>\(\dfrac{NQ}{NM}=\dfrac{MQ}{PM}=\dfrac{4,8}{6}=\dfrac{4}{5}\)
=> \(\dfrac{S_{MQN}}{S_{NMP}}=\left(\dfrac{4}{5}\right)^2=\dfrac{16}{25}\)
Hình vẽ hơi xấu thông cảm nha...