Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
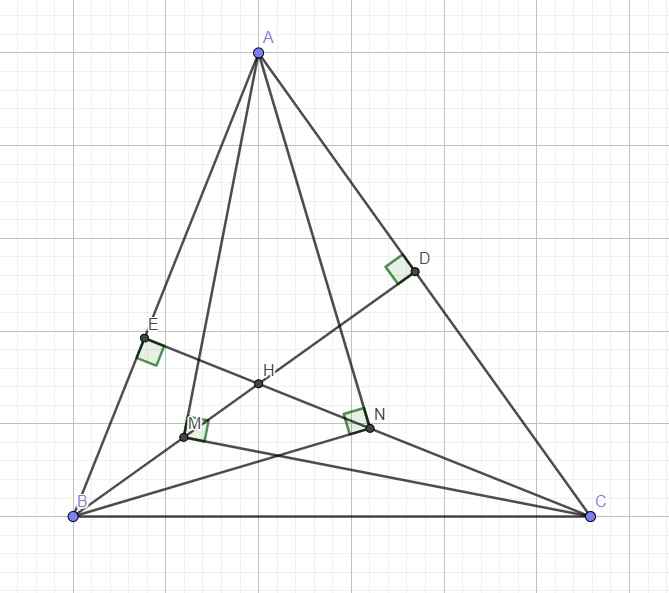
Tam giác AMC vuông tại M với đường cao MD
Áp dụng hệ thức lượng: \(AM^2=AD.AC\) (1)
Tương tự ta có:
\(AN^2=AE.AB\) (2)
Mặt khác xét hai tam giác vuông ABD và ACE có:
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta_VABD\sim\Delta_VACE\) (g.g)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Leftrightarrow AB.AE=AC.AD\) (3)
(1);(2);(3) \(\Rightarrow AM^2=AN^2\) \(\Rightarrow AM=AN\)
Bài 2 tham khảo tại đây:
Cho tam giác ABC vuông tại A , đường cao AH . Biết AB/AC = 20/21 , AH = 420 . Tính chu vi tam giác ABC - Hoc24

a, \(vì\)AD là phân giác suy ra góc BAD =góc DAC =45 ĐỘ
cos45 độ = AD/AB =4 /AB =1/ căn 2 suy ra AB =4 NHÂN CĂN 2
TH TỰ dùng sin 45 độ =dc/ac =5/ad =1/căn 2 suy ra AC =5 CĂN 2 ÁP DỤNG PITA GO TÌM RA CẠNH bc
b,

Do: Góc ABD = Góc ACE (= 90 - A)
=> Δ ABD ∼ Δ ACE (2 Δ vuông)
=> AD.AC = AE.AB (tỉ lệ đồng dạng)
<=> AM2 = AN2 (Hệ thức lượng trong Δ vuông)
<=> AM = AN
Hay Δ AMN cân tại A.=>....

a) Ta có: \(\angle BEC=\angle BDC=90\Rightarrow BCDE\) nội tiếp \(\Rightarrow\angle ADE=\angle ABC\)
Xét \(\Delta ADE\) và \(\Delta ABC:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\angle ADE=\angle ABC\end{matrix}\right.\)
\(\Rightarrow\Delta ADE\sim\Delta ABC\left(g-g\right)\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\Rightarrow AD.AC=AE.AB\)
b) Vì \(\Delta AMC\) vuông tại M có \(MD\bot AC\Rightarrow AM^2=AD.AC\)
Vì \(\Delta ANB\) vuông tại N có \(NE\bot AB\Rightarrow AN^2=AE.AB\)
mà \(AE.AB=AD.AC\Rightarrow AM^2=AN^2\Rightarrow AM=AN\)
\(\Rightarrow\Delta AMN\) cân tại A
c) Từ D kẻ đường thẳng vuông góc với DE cắt CE tại F
Xét \(\Delta DEF\) và \(\Delta DBC:\) Ta có: \(\left\{{}\begin{matrix}\angle EDF=\angle BDC=90\\\angle DEF=\angle DBC\left(BEDCnt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta DEF\sim\Delta DBC\left(g-g\right)\Rightarrow\dfrac{DE}{EF}=\dfrac{DB}{BC}\Rightarrow DE.BC=DB.EF\)
Ta có: \(\angle EDF-\angle BDF=\angle CDB-\angle BDF\left(=90-\angle BDF\right)\)
\(\Rightarrow\angle EDB=\angle CDF\)
Xét \(\Delta DEB\) và \(\Delta DFC:\) Ta có: \(\left\{{}\begin{matrix}\angle EDB=\angle FDC\\\angle DCF=\angle DBE\left(BEDCnt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta DEB\sim\Delta DFC\left(g-g\right)\Rightarrow\dfrac{CF}{BE}=\dfrac{CD}{BD}\Rightarrow BE.CD=BD.CF\)
\(\Rightarrow BE.CD+DE.BC=BD.CF+BD.EF=BD\left(CF+EF\right)\)
\(=BD.CE\)

3. A B C D P Q I
Trên tia đối của tia BA lấy I sao cho BI = DQ
\(\Delta DCQ=\Delta BCI\left(c.g.c\right)\Rightarrow\hept{\begin{cases}CQ=CI\\\widehat{DCQ}=\widehat{BCI}\end{cases}}\)
Ta có: \(\widehat{QCI}=\widehat{QCB}+\widehat{BCI}=\widehat{QCB}+\widehat{DCQ}=\widehat{BCD}=90^0\)
Ta có: \(AP+AQ+PQ=2AB\)
\(\Rightarrow AP+AQ+PQ=AP+PB+AQ+QD\)
\(\Rightarrow PQ=PB+QD\)
\(\Rightarrow PQ=PB+BI\Rightarrow PQ=PI\)
\(\Delta PCQ=\Delta PCI\left(c.c.c\right)\Rightarrow\widehat{PCQ}=\widehat{PCI}=\frac{\widehat{QCI}}{2}=\frac{90^0}{2}=45^0\)