Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, đồng dạng trường hợp góc - góc
b, Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền nên ta có :
AM = BM = CM = BC/2 = (BH + CH )/ 2 = 13/2 = 6,5 ( cm )
ta có : HM = BM - BH = 6,5 - 4 = 2,5 ( cm )
áp dụng định lí Pytago cho tam giác vuông AHM ta có : \(AH^2=AM^2-HM^2\Rightarrow AH=\sqrt{AM^2-HM^2}=\sqrt{6,5^2-2,5^2}=6.\) (cm )
\(S_{AMH}=\frac{AH.HM}{2}=\frac{6.2,5}{2}=7,5\left(cm^2\right)\)

Xét hai tam giác vuông HBA,HAC có:
∠ (BHA) = ∠ (AHC) = 90 0
∠ B = ∠ (HAC) (hai góc cùng phụ ∠ C )
⇒ △ HBA đồng dạng △ HAC (g.g)
Suy ra: 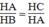
⇒ H A 2 = HB.HC = 4.9 = 36(cm)
Suy ra: AH = 6(cm)
Lại có: BM = 1/2 BC = 1/2 .(9+4) = 1/2 .13 = 6,5cm
Mà HM = BM – BH = 6,5 – 4 = 2,5cm
Vậy S A H M = 1/2 AH.HN = 1/2 .6.2,5 = 7,5 c m 2

Ta có BH=4 ; CH=9 =>BC = 13
Vì AM là đường trung tuyến nên AM = MC = BC/2 = 6.5
Ta có HM = BC-( BH + MC ) = 2,5
lại có AM là đường trung tuyến nên AM = BC/2 = 6,5
Xét tam giác vuông AHM : AH^2 = AM^2 - HM^2
=>. AH = 6
S tam giác AMH = 1/2.AH.HM = 7,5
──────▄▌▐▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▌
───▄▄██▌█ ░Xe chở 100000000 đến đây..
▄▄▄▌▐██▌█ ░░░░░░ ░░░░░░░░░ ░░░░░░░▐\.
███████▌█▄▄▄▄▄▄ ▄▄▄▄▄▄▄▄▄▄▄▄▄▄▄ ▄▄▌ \.
▀❍▀▀▀▀▀▀▀❍❍▀▀▀▀ ▀▀▀▀▀▀▀▀▀▀▀❍❍ ▀▀.
░░░░░░███████ ]▄▄▄▄▄▄▄▄▃
▂▄▅█████████▅▄▃▂
I███████████████████].
◥⊙▲⊙▲⊙▲⊙▲⊙▲⊙▲⊙◤…
Bằng chíu

a)
Ta có \(\Delta ABC\approx\Delta HBA\)vì hai tam giác vuông này có chung góc nhọn B
Lại có \(\Delta ABC\approx\Delta HAC\)có chung góc nhọn C
\(\Rightarrow\Delta HBA\approx\Delta HAC\)(tính chất bắc cầu)
b)Ta có AM là trung tuyến nên \(BM=\frac{1}{2}\left(BH+CH\right)=\frac{13}{2}\)
\(HM=BM-BH=\frac{13}{2}-4=\frac{5}{2}\)
Vì \(\Delta HBA\approx\Delta HAC\)nên
\(\frac{HB}{HA}=\frac{HA}{HC}\Rightarrow\frac{4}{HA}=\frac{HA}{9}\)
\(\Rightarrow HA^2=36\Rightarrow HA=6\)
\(S_{ABC}=\frac{\frac{5}{2}\cdot6}{2}=\frac{15}{2}\left(cm^2\right)\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=BH\cdot CH\)
\(\Leftrightarrow AH^2=4\cdot9=36\)
hay AH=6(cm)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=4+9=13(cm)
Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(AM=\dfrac{1}{2}BC\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
hay \(AM=\dfrac{1}{2}\cdot13=6.5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAMH vuông tại H, ta được:
\(AM^2=AH^2+MH^2\)
\(\Leftrightarrow MH^2=AM^2-AH^2=6.5^2-6^2=6.25\)
hay MH=2,5(cm)
Diện tích tam giác AMH là:
\(S_{AMH}=\dfrac{AH\cdot HM}{2}=\dfrac{6\cdot2.5}{2}=\dfrac{15}{2}=7.5\left(cm^2\right)\)

a, Xét Δ ABC và Δ CBH
Ta có : \(\widehat{ACB}=\widehat{CHB}=90^o\)
\(\widehat{ABC}=\widehat{CBH}\) (góc chung)
=> Δ ABC ∾ Δ CBH (g.g)
b, Ta có : Δ ABC ∾ Δ CBH (cmt)
=> \(\dfrac{AB}{CB}=\dfrac{BC}{BH}\)
=> \(BC^2=AB.BH\)
c,
Ta có : AB = AH + HB
=> AB = 4 + 9
=> AB = 13 (cm)
Ta có : \(BC^2=AB.BH\left(cmt\right)\)
=> \(BC^2=13.9\)
=> \(BC^2=117\)
=> BC = 10,8 (cm)
Xét Δ ABC
Ta có : \(AB^2=AC^2+BC^2\)
=> \(13^2=AC^2+10,8^2\)
=> \(169=AC^2+116,64\)
=> \(169-116,64=AC^2\)
=> \(52,36=AC^2\)
=> AC = 7,2 (cm)
Xét Δ ABC vuông tại C
=> \(S_{\Delta ABC}=\dfrac{AC.BC}{2}\)
=> \(S_{\Delta ABC}=\dfrac{7,2.10,8}{2}\)
=> \(S_{\Delta ABC}=38,88\left(cm^2\right)\)
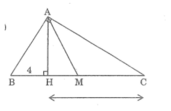

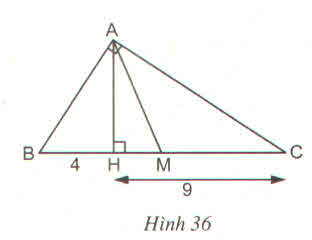


a,
Xét Δ AHB và Δ CAB, có :
\(\widehat{AHB}=\widehat{CAB}=90^o\)
\(\widehat{ABH}=\widehat{CBA}\) (góc chung)
=> Δ AHB ∾ Δ CAB (g.g)
=> \(\dfrac{AH}{CA}=\dfrac{HB}{AB}\)
=> \(\dfrac{AB}{CA}=\dfrac{HB}{AH}\)
Xét Δ AHB và Δ CHA, có :
\(\widehat{AHB}=\widehat{CHA}=90^o\)
\(\dfrac{AB}{CA}=\dfrac{HB}{AH}\) (cmt)
=> Δ AHB ∾ Δ CHA (g.g)
=> \(\dfrac{AH}{CH}=\dfrac{HB}{HA}\)
=> \(AH^2=HB.CH\)
b, Ta có : \(AH^2=BH.CH\) (cmt)
=> \(AH^2=4.9\)
=> \(AH^2=36\)
=> AH = 6
Xét Δ AHB, có :
\(AB^2=AH^2+BH^2\)
=> \(AB^2=6^2+4^2\)
=> \(AB^2=52\)
=> AB = 7,2 (cm)
Xét Δ AHC, có :
\(AC^2=AH^2+CH^2\)
=> \(AC^2=6^2+9^2\)
=> \(AC^2=117\)
=> AC = 10,8 (cm)
Xét Δ ABC, có :
\(BC^2=AB^2+AC^2\)
=> \(BC^2=7,2^2+10,8^2\)
=> \(BC^2=168,48\)
=> BC = 12,9 (cm)
Ta có : MC = \(\dfrac{1}{2}BC\) (M là trung điểm BC do có đường trung tuyến AM)
=> MC = 6,45 (cm)
Ta có : BC = BH + HM + MC
=> 12,9 = 4 + HM + 6,45
=> HM = 12,9 - 4 - 6,45
=> HM = 2,45 (cm)
Xét Δ AMH vuông tại H, có :
\(S_{\Delta AMH}=\dfrac{1}{2}AH.HM\)
=> \(S_{\Delta AMH}=\dfrac{1}{2}.6.2,45\)
=> \(S_{\Delta AMH}=7,35\left(cm\right)\)