Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a: BC=17cm
AH=120/7(cm)
b: Xét tứ giác AMHN có góc AMH=góc ANH=góc MAN=90 độ
nên AMHN là hình chữ nhật
Suy ra: AH=MN=120/7(cm)
c: Xét ΔAHB vuông tại H có HM là đường cao
nen \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

a: AD=DC=6/2=3cm
BD=căn 8^2+3^2=căn 73(cm)
DM là phân giác
=>BM/BD=MA/AD
=>BM/căn 73=MA/3=(BM+MA)/(căn 73+3)=8/căn 73+3
=>BM=8*căn 73/3+căn 73(cm)
b: Xét ΔBAD có DM là phân giác
nen BM/MA=BD/DA=BD/DC
Xét ΔBDC có DN là phân giác
nên BN/NC=BD/DC
=>BM/MA=BN/NC
=>MN//AC
c: Xét tứ giác MNCA có MN//CA và góc MAC=90 độ
nên MNCA là hình thang vuông

b) Xét ΔBDA có
DM là đường phân giác ứng với cạnh AB
nên \(\dfrac{BM}{MA}=\dfrac{BD}{DA}\)(1)
Xét ΔBDC có
DN là đường phân giác ứng với cạnh BC
nên \(\dfrac{BN}{NC}=\dfrac{BD}{DC}\)(2)
Ta có: D là trung điểm của AC(gt)
nên DA=DC(3)
Từ (1), (2) và (3) suy ra \(\dfrac{BM}{MA}=\dfrac{BN}{NC}\)
hay MN//AC(Định lí Ta lét đảo)
c) Xét tứ giác MNCA có MN//AC(cmt)
nên MNCA là hình thang
mà \(\widehat{MAC}=90^0\)
nên MNCA là hình thang vuông

Bài 1:
a: \(BC=\sqrt{8^2+15^2}=17\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{60}{17}\left(cm\right)\)
b: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
SUy ra: AH=MN=60/17(cm)
c: Xét ΔAHB vuông tại H có HM là đừog cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xet ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

1.a. Áp dụng định lí Pytago vào \(\Delta ABC\) (\(\widehat{A}\) =90o) có:
\(BC=\)\(\sqrt{AB^2+AC^2}\) \(=\) \(\sqrt{8^2+15^2}\) \(=\sqrt{64+225}\) \(=\sqrt{289}\) \(=17\) \(\left(cm\right)\)
Vậy BC=17cm
mk chỉ tính được BC thôi
2a. Áp dụng định lí Pytago vào \(\Delta ABD\) (\(\widehat{BAD}\) =90o) có:
\(BD=\sqrt{AB^2+AD^2}=\sqrt{8^2+6^2}=\sqrt{64+36}=\sqrt{100}=10\) (cm)
Vậy BD=10cm
mk chỉ tính được BD thôi



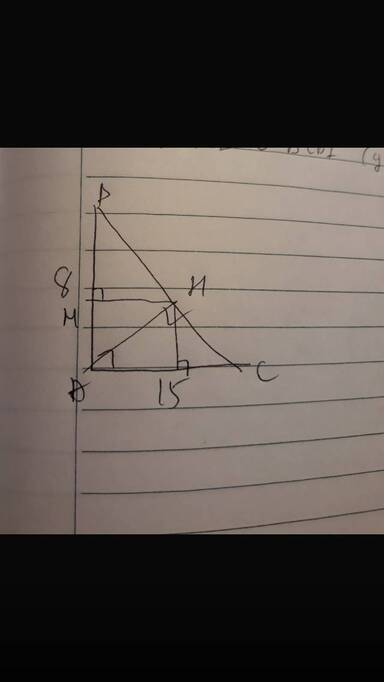
Bài 1:
a: \(BC=\sqrt{8^2+15^2}=17\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{120}{17}\left(cm\right)\)
b: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
Suy ra: AH=MN=120/17(cm)
c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)