Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Khi bớt ở cả tử số và mẫu số của một phân số thì hiệu giữa mẫu số và tử số của phân số đó không thay đổi. Vậy hiệu giữa mẫu số và tử số là:
47 - 23 = 24
Coi tử số mới là 7 phần bằng nhau thì mẫu số mới là 13 phần như thế, hiệu là 24.
Hiệu số phần bằng nhau là:
13 - 7 = 6 (phần)
Giá trị 1 phần là:
24 : 6 = 4
Tử số mới là:
4 . 7 = 28
Số nguyên cần tìm là:
23 - 28 = -5
Đáp số: -5

bài 1
a) Với a là số nguyên thì phân số a/71 tối giản khi n không thuộc ước hoặc bội của 71
b) Với a là số nguyên thì phân số a/225 tối giản khi b không thuộc ước hoặc bội của 225

Bài 1:
Giải:
Gọi số nguyên đó là a ( \(a\in Z\) )
Theo bài ra ta có:
\(\frac{23-a}{47-a}=\frac{7}{13}\Rightarrow\left(23-a\right).13=7.\left(47-a\right)\)
\(\Rightarrow299-13a=329-7a\)
\(\Rightarrow13a-7a=299-329\)
\(\Rightarrow6a=-30\)
\(\Rightarrow a=-5\)
Vậy số cần tìm là -5

3. Gọi d là ƯCLN(2n + 3, 4n + 8), d ∈ N*
\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\4n+8⋮d\end{cases}\Rightarrow\hept{\begin{cases}2\left(2n+3\right)⋮d\\4n+8⋮d\end{cases}\Rightarrow}\hept{\begin{cases}4n+6⋮d\\4n+8⋮d\end{cases}}}\)
\(\Rightarrow\left(4n+8\right)-\left(4n+6\right)⋮d\)
\(\Rightarrow2⋮d\)
\(\Rightarrow d\in\left\{1;2\right\}\)
Mà 2n + 3 không chia hết cho 2
\(\Rightarrow d=1\)
\(\RightarrowƯCLN\left(2n+3,4n+8\right)=1\)
\(\Rightarrow\frac{2n+3}{4n+8}\) là phân số tối giản.

Từ 
ab = 8a(b – a)
ab = 8ab – 8a2
8a2 = 7ab
8a = 7b hay

Giải từng bài
Bài 1 :
Ta có :
\(\frac{23+n}{40+n}=\frac{3}{4}\)
\(\Leftrightarrow\)\(4\left(23+n\right)=3\left(40+n\right)\)
\(\Leftrightarrow\)\(92+4n=120+3n\)
\(\Leftrightarrow\)\(4n-3n=120-92\)
\(\Leftrightarrow\)\(n=28\)
Vậy số cần tìm là \(n=28\)
Chúc bạn học tốt ~
Bài 2 :
\(a)\) Gọi \(ƯCLN\left(12n+1;30n+2\right)=d\)
\(\Rightarrow\)\(\hept{\begin{cases}12n+1⋮d\\30n+2⋮d\end{cases}\Rightarrow\hept{\begin{cases}5\left(12n+1\right)⋮d\\2\left(30n+2\right)⋮d\end{cases}\Rightarrow}\hept{\begin{cases}60n+5⋮d\\60n+4⋮d\end{cases}}}\)
\(\Rightarrow\)\(\left(60n+5\right)-\left(60n+4\right)⋮d\)
\(\Rightarrow\)\(1⋮d\)
\(\Rightarrow\)\(d\inƯ\left(1\right)=\left\{1;-1\right\}\)
\(\Rightarrow\)\(ƯCLN\left(12n+1;30n+2\right)=\left\{1;-1\right\}\)
Vậy \(A=\frac{12n+1}{30n+2}\) là phân số tối giản với mọi giá trị nguyên n
Chúc bạn học tốt ~
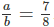
Bài 2:
Gọi số cần tìm là a
Theo đề, ta có: \(\dfrac{a+13}{a+19}=\dfrac{5}{7}\)
=>7a+91=5a+95
=>2a=4
hay a=2