Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chu vi hình vuông ABCD là :
3 * 4 = 12 ( cm )
Diện tích hình vuông ABCD là :
3 * 3 = 9 ( cm2 )
b) sai đề vì nối E với A thì mới ra hình thang, nếu không thì ra hình vuông với một cạnh kéo dài mà thôi

bài này sao khó vậy
mình không làm được đâu
nhưng cô của mình cũng ra bài giống y hệt nếu có người trả lời thì thông báo cho mình biết nha
thank you very much

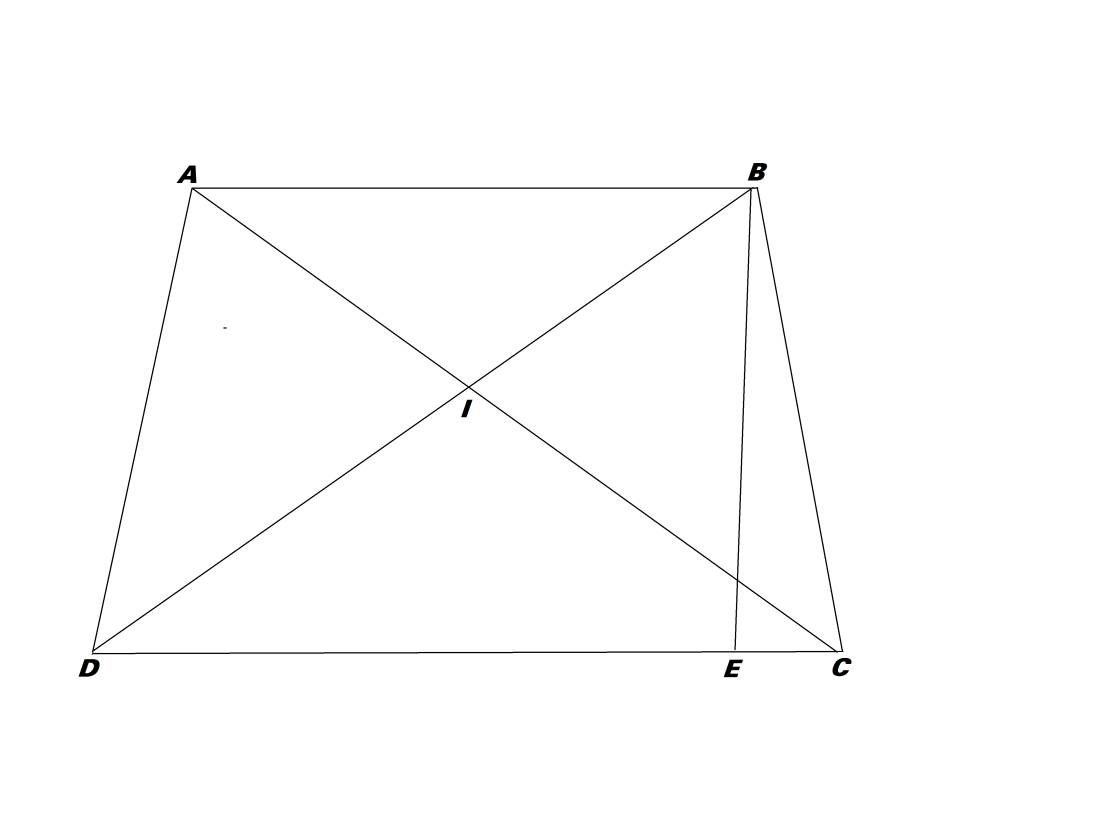
a)
\(S_{ADC}=S_{BDC}\) (vì có chung chiều cao và cạnh DC)
\(\Rightarrow S_{ADC}-S_{DIC}=S_{BDC}-S_{DIC}\)
\(\Rightarrow S_{ADI}=S_{BIC}\)
b)
Chiều cao hình thanh là:
\(\dfrac{14\times2}{4}=7\left(cm\right)\)
Diện tích hình thang ABCD là:
\(\dfrac{\left(9+22\right)\times7}{2}=108,5\left(cm^2\right)\)
c)
Độ dài DE là: \(22-4=18\left(cm\right)\)
\(\Rightarrow\dfrac{AB}{DE}=\dfrac{9}{18}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{S_{ABD}}{S_{BDE}}=\dfrac{1}{2}\) (có cùng chiều cao)