Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Với giả thiết ở đề bài, ta có thể tính được r từ đó tính được diện tích mặt cầu gần bằng \(26cm^2\)
b) Tương tự câu a, ta tính được thể tích hình nón là \(7,9cm^3\)

\(1.Sxq=\pi Rl=\pi3.5=15\pi cm^2\)
\(Stp=Sxq+\pi R ^2=15\pi+9\pi=24\pi cm^2\)
\(2.V=\dfrac{1}{3}\pi R^2.\sqrt{l^2-R^2}=\dfrac{1}{3}\pi.3^2.\sqrt{5^2-3^2}=12\pi cm^3\)

Đáp án D
Gọi l là độ dài đường sinh của hình nón.
Vì bán kính hình cầu và bán kính đáy của hình nón bằng nhau nên từ giả thiết ta có:
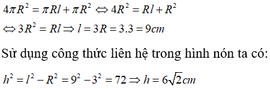

Đáp án D
Gọi l là độ dài đường sinh của hình nón.
Vì bán kính hình cầu và bán kính đáy của hình nón bằng nhau nên từ giả thiết ta có:
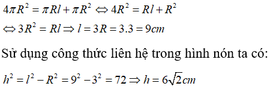

Câu 6:
\(V_1=\dfrac{1}{3}\cdot pi\cdot R^2\cdot h\)
\(V_2=\dfrac{1}{3}\cdot pi\cdot\left(2\cdot R\right)^2\cdot2h=\dfrac{4}{3}\cdot pi\cdot R^2\cdot h\)
=>Thể tích tăng thêm 4 lần

a, Tính được r = 1,44cm Þ Smc = 4p r 2 = 26,03 c m 2
b, Ta có V c = 4 3 πR 2 = 15 , 8 cm 3 => R = 1,56cm
=> V h n = 1 3 πR 2 h ≈ 2 , 53 πcm 3

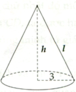

\(S_{\text{mặt đáy}}:\pi.3^2=9\pi\left(cm^2\right)\)
\(S_{\text{xung quanh}}:\pi rl=\pi.3.l=24\pi-9\pi=15\pi\Rightarrow l=5\left(cm^2\right)\)
\(\text{Chiều cao khối chóp}:h=\sqrt{l^2-r^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(V:\frac{1}{3}\pi r^2h=\frac{1}{3}\pi.3^2.4=12\pi\left(cm^3\right)\)
Diện tích mặt đáy là : \(\pi.3^2=9\pi(m^2)\)
Diện tích xung quanh là : \(S_{xq}=\pi rl=\pi.3.l=24\pi-9\pi=15\pi=>l=5(m)\)
Chiều cao của khối chóp là \(h=\sqrt{l^2-r^2}=\sqrt{5^2-3^2}=4(m)\)
Thể tích của hình nón là : \(V=\frac{1}{3}\pi r^2h=\frac{1}{3}\pi.3^2.4=12\pi(m^3)\)