Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=\dfrac{-1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
b) CG.CAN??

Do G là trọng tâm tam giác
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{1}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}+\dfrac{1}{3}\overrightarrow{AC}\)
\(=\dfrac{2}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}=-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\)
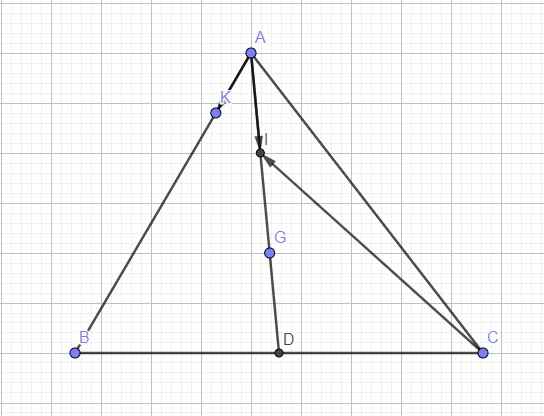
Do I là trung điểm AG
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AG}=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right)=-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{AK}=\dfrac{1}{5}\overrightarrow{AB}=\dfrac{1}{5}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)=-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)
\(\overrightarrow{CI}=\overrightarrow{CA}+\overrightarrow{AI}=\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{CK}=\overrightarrow{CA}+\overrightarrow{AK}=\overrightarrow{CA}-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}=\dfrac{4}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)

1) Ta có:\(\overrightarrow{AB}+\overrightarrow{DE}-\overrightarrow{DB}+\overrightarrow{BC}=\overrightarrow{AE}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{BE}+\overrightarrow{EC}\)
\(=\overrightarrow{AC}+\overrightarrow{BE}+\overrightarrow{CE}+\overrightarrow{EC}=\overrightarrow{AC}+\overrightarrow{BE}\left(đpcm\right)\)2) a) Ta có: \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{ED}+\overrightarrow{BF}+\overrightarrow{FE}+\overrightarrow{CD}+\overrightarrow{DF}\)\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}+\overrightarrow{ED}+\overrightarrow{DF}+\overrightarrow{FE}\)
\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\left(đpcm\right)\)
b) Ta có: \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{CB}+\overrightarrow{BD}\)
\(=\overrightarrow{AD}+\overrightarrow{CB}+\overrightarrow{DB}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{CB}\left(đpcm\right)\)c) \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AB}-\overrightarrow{BD}\)
\(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AB}+\overrightarrow{DB}\)
Ta có: \(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AB}+\overrightarrow{DB}+\overrightarrow{BC}\) ( đề bài bị lỗi gì à ?? :v ) hay do mình =))

Gọi M là trung điểm EF
\(\overrightarrow{BM}=\dfrac{1}{2}\overrightarrow{BE}+\dfrac{1}{2}\overrightarrow{BF}=-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{CF}\right)\)
\(=-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}-\dfrac{1}{4}\overrightarrow{AB}=-\dfrac{7}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
\(\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BM}=-\dfrac{7}{6}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AD}\)
\(\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}=-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AD}\)
\(\overrightarrow{DG}=\overrightarrow{DA}+\overrightarrow{AG}=-\overrightarrow{AD}+\overrightarrow{AG}=-\dfrac{1}{6}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AD}\)

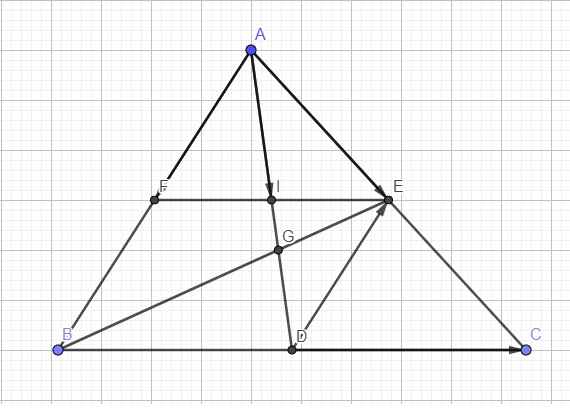
F là trung điểm AB \(\Rightarrow\overrightarrow{AF}=\dfrac{1}{2}\overrightarrow{AB}\) ; E là trung điểm AC \(\Rightarrow\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AC}\)
Ta có EF song song BC (đường trung bình)
Mà D là trung điểm BC \(\Rightarrow\) I là trung điểm EF \(\Rightarrow AI\) là trung tuyến tam giác AEF
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AE}+\dfrac{1}{2}\overrightarrow{AF}\)
Theo tính chất trọng tâm:
\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{2}{3}\left(\overrightarrow{AE}+\overrightarrow{AF}\right)=\dfrac{2}{3}\overrightarrow{AE}+\dfrac{2}{3}\overrightarrow{AF}\)
DE là đường trung bình tam giác ABC
\(\Rightarrow\overrightarrow{DE}=\dfrac{1}{2}\overrightarrow{BA}=-\dfrac{1}{2}\overrightarrow{AB}=-\overrightarrow{AE}\) hay \(\overrightarrow{DE}=-\overrightarrow{AE}+0.\overrightarrow{AF}\)
D là trung điểm BC \(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{AC}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}=-\overrightarrow{AE}+\overrightarrow{AF}\)
Câu 1:
A B C D I G
\(\overrightarrow{BI}=\frac{1}{2}\overrightarrow{BD}+\frac{1}{2}\overrightarrow{BC}\\ =\frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{AD}\right)+\frac{1}{2}\overrightarrow{BC}\\ =\frac{1}{2}\left(-\overrightarrow{AB}+\overrightarrow{AD}\right)+\frac{1}{2}\overrightarrow{AD}\\ =-\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AD}\\ =-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}=-\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}\)
\(\overrightarrow{CG}=\frac{1}{3}\overrightarrow{CC}+\frac{1}{3}\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CD}\\ =-\frac{1}{3}\overrightarrow{AD}-\frac{1}{3}\overrightarrow{AB}=-\frac{1}{3}\overrightarrow{b}-\frac{1}{3}\overrightarrow{a}\)
A B C G E D
\(a\text{) }\overrightarrow{DE}=\overrightarrow{DA}+\overrightarrow{AE}=-2\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}\\ \overrightarrow{DG}=\overrightarrow{DA}+\overrightarrow{AG}\\ =-2\overrightarrow{AB}+\frac{1}{3}\left(\overrightarrow{AA}+\overrightarrow{AB}+\overrightarrow{AC}\right)\\ =-2\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\\ =-\frac{5}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\)
\(\text{b) }\overrightarrow{DG}=-\frac{5}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}=\frac{5}{6}\left(-2\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}\right)=\frac{5}{6}\overrightarrow{DE}\)
=> D;G;E thẳng hàng
c) \(\overrightarrow{KA}+\overrightarrow{KB}+3\overrightarrow{KC}=2\overrightarrow{KD}\)
\(\Rightarrow\overrightarrow{KA}+\overrightarrow{KB}+\overrightarrow{KC}=2\overrightarrow{KD}-2\overrightarrow{KC}\\ \Rightarrow3\overrightarrow{KG}=2\left(\overrightarrow{KD}-\overrightarrow{KC}\right)\\ \Rightarrow3\overrightarrow{KG}=2\overrightarrow{CD}\\ \Rightarrow\overrightarrow{KG}=\frac{2}{3}\overrightarrow{CD}\\ \Rightarrow\overrightarrow{KG}\text{ cùng phương }\overrightarrow{CD}\\ \Rightarrow KG//CD\)