Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bỏ qua nhiệt độ làm ấm vỏ điện và nhiệt lượng tỏa ra môi trường ngoài.
\(\Rightarrow Q_{toa}=Q_{thu}=mc\Delta t=2\cdot4200\cdot80=672000\left(J\right)\)
Ta có: \(Q_{toa}=A=Pt\Rightarrow t=\dfrac{Q_{toa}}{P}=\dfrac{672000}{1000}=672\left(s\right)\)
Vậy....................
Nhiệt lượng bếp tỏa:
\(Q=mc\Delta t=2\cdot4200\cdot\left(100-20\right)=672000J\)
Điện trở ấm:
\(R=\dfrac{U^2}{P}=\dfrac{220^2}{1000}=48,4\Omega\)
Dòng điện qua ấm:
\(I=\dfrac{U}{R}=\dfrac{220}{48,4}=\dfrac{50}{11}A\)
Thời gian cần để đun ấm:
\(t=\dfrac{A}{R\cdot I^2}=\dfrac{Q}{R\cdot I^2}=\dfrac{672000}{48,4\cdot\left(\dfrac{50}{11}\right)^2}=672s\)

a) Nhiệt lượng cần cung cấp để đun sôi lượng nước trên là:
Qi = cm(t2 – t1) = 4200.2.(100-20) = 672000 J
b) Nhiệt lượng mà ấm đã tỏa ra khi đó là:
Từ công thức H = => Qtp =
= 746700 J
c) Thòi gian đun sôi lượng nước trên là:
Từ công thức Qtp = A = Pt, ta tìm được t = ≈ 747 s
a) Nhiệt lượng cần cung cấp để đun sôi lượng nước trên là:
Qi = cm(t2 – t1) = 4200.2.(100-20) = 672000 \(j\)
b) Nhiệt lượng mà ấm đã tỏa ra khi đó là:
Từ công thức H = => Qtp =
= 746700 J
c) Thòi gian đun sôi lượng nước trên là:
Từ công thức Qtp = A = Pt, ta tìm được t ≈ 747 s

a) Nhiệt lượng cần cung cấp để đun sôi lượng nước trên là:
Q1 = c.m.(T – T0) = 4200.2.(100 - 20) = 672000 (J)
b) Hiệu suất của bếp: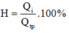
Nhiệt lượng mà ấm điện đã tỏa ra khi đó là:
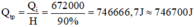
c) Từ công thức: Qtp = A = P.t
→ Thời gian đun sôi lượng nước:
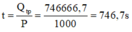
a) Nhiệt lượng cần cung cấp để đun sôi lượng nước trên là:
Q1 = c.m.(T – T0) = 4200.2.(100 - 20) = 672000 (J)
b) Hiệu suất của bếp: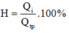

Nhiệt lượng cung cấp để đun sôi nước:
\(A=Q=mc\Delta t=5\cdot4200\cdot\left(100-20\right)=1680000J\)
Thời gian đun sôi nước:
\(t=\dfrac{A}{UI}=\dfrac{1680000}{220\cdot\dfrac{1000}{220}}=1680s\)
Chọn D

Ấm điện được dùng hiệu điện thế đúng bằng hiệu điện thế định mức nên công suất P của nó cũng chính bằng công suất định mức (1000W).
Bỏ qua nhiệt lượng làm nóng vỏ ấm và nhiệt lượng tỏa vào môi trường, nên nhiệt lượng Q để đun sôi nước sẽ chính bằng lượng điện năng A mà ấm đã tiêu thụ. Ta có A = Q, tức là Pt = cm(t2 – t1), từ đó suy ra
t = = 672 s.
Ấm điện được dùng hiệu điện thế đúng bằng hiệu điện thế định mức nên công suất P của nó cũng chính bằng công suất định mức (1000W).
Bỏ qua nhiệt lượng làm nóng vỏ ấm và nhiệt lượng tỏa vào môi trường, nên nhiệt lượng Q để đun sôi nước sẽ chính bằng lượng điện năng A mà ấm đã tiêu thụ.
Ta có:
+ A=PtA=Pt
+ Q=mcΔtQ=mcΔt
Lại có:
A=QA=Q, tức là Pt=cm(t2–t1)Pt=cm(t2–t1), từ đó suy ra:
t=cm(t2−t1)P=4200.2(100−20)1000=672st=cm(t2−t1)P=4200.2(100−20)1000=672s.

Vì hiệu điện thế định mức của ấm bằng hiệu điện thế được sử dụng nên ấm hoạt động bình thường


Vì bỏ qua nhiệt lượng làm ấm vỏ và nhiệt lượng tỏa ra môi trường ngoài, nên: \(Q_{toa}=Q_{thu}=mc\Delta t=6\cdot4200\cdot80=2016000\left(J\right)\)
Ta có: \(Q_{toa}=A=UIt\Rightarrow t=\dfrac{Q_{toa}}{UI}=\dfrac{2016000}{220\cdot\dfrac{1000}{220}}=2016\left(s\right)=33min6s\)