K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AP
0
11 tháng 4 2018
Đề bài đâu bạn:
Với mik cx ko bít giải phương trình đâu
Hihi
:3))
DD
Đoàn Đức Hà
Giáo viên
15 tháng 5 2021
1) \(2x-\left|6x-7\right|=-x+8\)
\(\Rightarrow\orbr{\begin{cases}2x-\left(6x-7\right)=-x+8\\2x-\left(-6x+7\right)=-x+8\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}-3x=1\\9x=15\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{3}\\x=\frac{5}{3}\end{cases}}\)
Thử lại đều không thỏa mãn.
Vậy phương trình vô nghiệm.
2) \(\frac{\left|x+2\right|}{2}-\frac{\left|x-1\right|}{3}=\frac{1}{4}+\frac{x+3}{6}\)(2)
Với \(x\ge1\): (2) tương đương với:
\(\frac{x+2}{2}-\frac{x-1}{3}=\frac{1}{4}+\frac{x+3}{6}\)
\(\Leftrightarrow0x=-\frac{7}{12}\)(phương trình vô nghiệm)
Với \(-2\le x< 1\): (2) tương đương với:
\(\frac{x+2}{2}-\frac{1-x}{3}=\frac{1}{4}+\frac{x+3}{6}\)
\(\Leftrightarrow\frac{2}{3}x=\frac{1}{12}\Leftrightarrow x=\frac{1}{8}\)(thỏa mãn)
Với \(x< -2\): (2) tương đương với:
\(\frac{-x-2}{2}-\frac{1-x}{3}=\frac{1}{4}+\frac{x+3}{6}\)
\(\Leftrightarrow\frac{-1}{3}x=\frac{25}{12}\Leftrightarrow x=-\frac{25}{4}\)(thỏa mãn)
DD
Đoàn Đức Hà
Giáo viên
15 tháng 5 2021
3) \(\left|x^2-2x\right|=x\)
\(\Rightarrow\orbr{\begin{cases}x^2-2x=x\\x^2-2x=-x\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2-3x=0\\x^2-x=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=0,x=3\\x=0,x=1\end{cases}}\)
Thử lại đều thỏa mãn.
4) \(\left|x^2-4x+5\right|=x^2-1\)
\(\Leftrightarrow x^2-4x+5=x^2-1\)(vì \(x^2-4x+5=\left(x-2\right)^2+1>0\))
\(\Leftrightarrow-4x=-6\)
\(\Leftrightarrow x=\frac{3}{2}\)
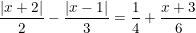
Với mọi a;b;c ta có
\(\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge2\left(a+b+c\right)-3\) (1)
Lại có:
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
\(\Leftrightarrow2a^2+2b^2+2c^2\ge2ab+2bc+2ca\)
\(\Leftrightarrow6a^2+6b^2+6c^2\ge6ab+6bc+6ca\) (2)
Cộng vế (1) và (2):
\(7\left(a^2+b^2+c^2\right)\ge2\left(a+b+c+3ab+3bc+3ca\right)-3=2.12-3=21\)
\(\Rightarrow a^2+b^2+c^2\ge3\)
Dấu "=" xảy ra khi \(a=b=c=1\)