K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LH
0
13 tháng 9
Đặt A'B'=a
ΔA'B'C' vuông tại B'
=>\(\left(A^{\prime}B^{\prime}\right)^2+\left(B^{\prime}C^{\prime}\right)^2=\left(A^{\prime}C^{\prime}\right)^2\)
=>\(\left(A^{\prime}C^{\prime}\right)^2=a^2+a^2=2a^2\)
=>\(A^{\prime}C^{\prime}=a\sqrt2\) (1)
Vì ABCD.A'B'C'D' là hình lập phương
nên A'A//C'C và A'A=C'C
=>A'ACC' là hình bình hành
=>A'C'//AC
=>\(\hat{AC;A^{\prime}D}=\hat{A^{\prime}C^{\prime};A^{\prime}D}=\hat{DA^{\prime}C^{\prime}}\)
A'B'C'D' là hình vuông
=>A'D'=D'C'=C'B'=A'B'=a
Vì ABCD.A'B'C'D' là hình lập phương
nên A'B'BA là hình vuông
=>A'A=A'B'=a
Vì ABCD.A'B'C'D' là hình lập phương
nên D'D=A'A=a
ΔA'D'D vuông tại D'
=>\(\left(D^{\prime}A^{\prime}\right)^2+\left(D^{\prime}D\right)^2=\left(A^{\prime}D\right)^2\)
=>\(\left(A^{\prime}D\right)^2=a^2+a^2=2a^2\)
=>\(A^{\prime}D=a\sqrt2\)
D'C'CD là hình vuông
=>\(\left(DC^{\prime}\right)^2=\left(D^{\prime}D\right)^2+\left(D^{\prime}C^{\prime}\right)^2=a^2+a^2=2a^2\)
=>\(DC^{\prime}=a\sqrt2\)
=>DC'=DA'=A'C'
=>ΔDA'C' đều
=>\(\hat{DA^{\prime}C^{\prime}}=60^0\)
=>\(\hat{AC;A^{\prime}D}=60^0\)
=>Chọn C
LA
9 tháng 1 2024
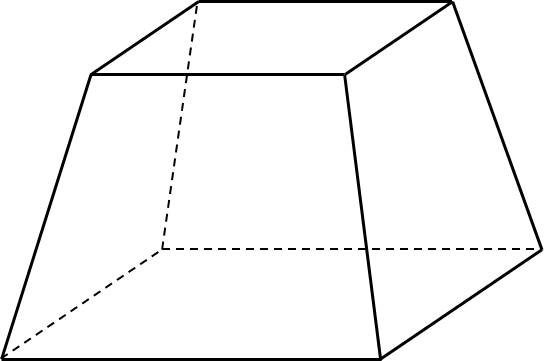
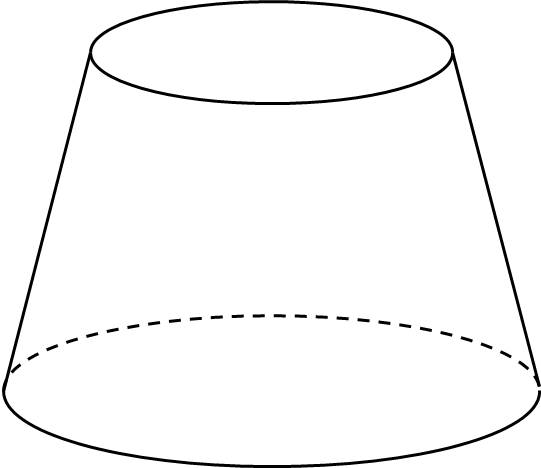
Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.
13 tháng 9
Câu 1: \(\frac{\pi}{2}<\alpha,\beta<\pi\)
=>\(\sin\alpha>0;\sin\beta>0;cos\alpha<0;cos\beta<0\)
\(\sin^2\alpha+cos^2\alpha=1\)
=>\(cos^2\alpha=1-\sin^2\alpha=1-\left(\frac13\right)^2=\frac89\)
mà \(cos\alpha<0\)
nên \(cos\alpha=-\frac{2\sqrt2}{3}\)
Ta có: \(\sin^2\beta+cos^2\beta=1\)
=>\(\sin^2\beta=1-\left(-\frac23\right)^2=1-\frac49=\frac59\)
mà \(\sin\beta>0\)
nên \(\sin\beta=\frac{\sqrt5}{3}\)
\(\sin\left(\alpha+\beta\right)=\sin\alpha\cdot cos\beta+cos\alpha\cdot\sin\beta\)
\(=\frac13\cdot\frac{-2}{3}+\frac{-2\sqrt2}{3}\cdot\frac{\sqrt5}{3}=\frac{-\sqrt2-2\sqrt{10}}{9}\)
Câu 2:
\(P=cos\left(a+b\right)\cdot cos\left(a-b\right)\)
\(=\frac12\cdot\left\lbrack cos\left(a+b+a-b\right)+cos\left(a+b-a+b\right)\right\rbrack=\frac12\cdot\left\lbrack cos2a+cos2b\right\rbrack\)
\(=\frac12\cdot\left\lbrack2\cdot cos^2a-1+2\cdot cos^2b-1\right\rbrack=cos^2a+cos^2b-1\)
\(=\left(\frac13\right)^2+\left(\frac14\right)^2-1=\frac19+\frac{1}{16}-1=\frac{25}{144}-1=-\frac{119}{144}\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a)
Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng lớn (dần tới \( + \infty \)).
b)
Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng bé (dần tới \( - \infty \)).
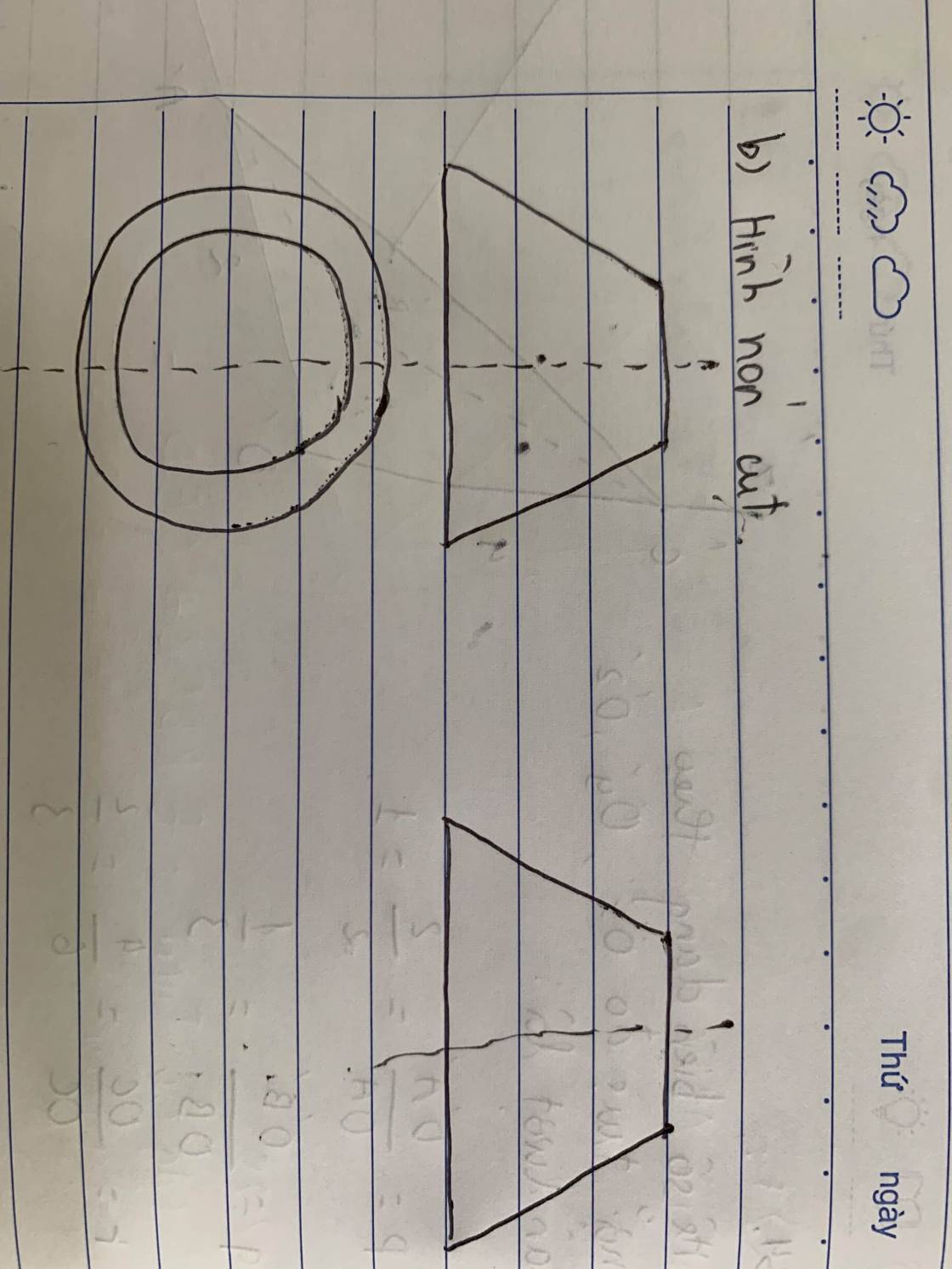
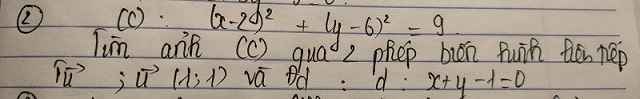
a.
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp BD\\BD\perp AC\left(\text{hai đường chéo hv}\right)\end{matrix}\right.\)
\(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp SA\)
Mà \(SA\perp OP\left(gt\right)\)
\(\Rightarrow SA\perp\left(PBD\right)\)
b.
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\Rightarrow OC=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow SO=\sqrt{SC^2-OC^2}=\dfrac{a\sqrt{14}}{2}\)
\(V=\dfrac{1}{3}SO.AB.AD=\dfrac{a^3\sqrt{14}}{6}\)
c.
Chắc đề ghi nhầm, (SCD) là mặt chứ đâu phải đường
Gọi E là trung điểm CD, tam giác SCD cân tại S \(\Rightarrow SE\perp CD\)
Tam giác OCD cân tại O \(\Rightarrow OE\perp CD\)
\(\Rightarrow CD\perp\left(SOE\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SEO}\) là góc giữa (SCD) và (ABCD)
\(OE=\dfrac{1}{2}AD=\dfrac{a}{2}\) (đường trung bình)
\(tan\widehat{SEO}=\dfrac{SO}{OE}=\sqrt{14}\Rightarrow\widehat{SEO}\approx75^02'\)
d.
\(\left\{{}\begin{matrix}AO\cap\left(SCD\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)\)
Trong tam giác vuông SEO, từ O kẻ \(OH\perp SE\) (1)
Theo cmt, \(CD\perp\left(SEO\right)\Rightarrow CD\perp OH\) (2)
(1);(2) \(\Rightarrow OH\perp\left(SCD\right)\Rightarrow OH=2\left(O;\left(SCD\right)\right)\)
Hệ thức lượng:
\(OH=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{210}}{30}\)
\(\Rightarrow d\left(A;\left(SCD\right)\right)=2OH=\dfrac{a\sqrt{210}}{15}\)
//Ko hiểu đề cho 2 điểm M và N làm gì, ko liên quan gì đến toàn bộ 4 câu hỏi luôn