
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn tham khảo:
Cho bất phương trình x2-6x +2(m+2)|x-3| +m2 +4m +12 >0có bao nhiêu giá trị nguyên của m ϵ [-10;10] để bất phương tình... - Hoc24

Câu a bạn coi lại đề
b. ĐKXĐ: \(x\ge0;x\ne1\)
\(\Leftrightarrow\dfrac{\sqrt{2x+1}+\sqrt{3x}}{1-x}=\dfrac{\sqrt{3x+2}}{1-x}\)
\(\Leftrightarrow\sqrt{2x+1}+\sqrt{3x}=\sqrt{3x+2}\)
\(\Leftrightarrow5x+1+2\sqrt{3x\left(2x+1\right)}=3x+2\)
\(\Leftrightarrow2\sqrt{6x^2+3x}=1-2x\) (\(x\le\dfrac{1}{2}\) )
\(\Leftrightarrow4\left(6x^2+3x\right)=4x^2-4x+1\)
\(\Leftrightarrow20x^2+16x-1=0\)
\(\Rightarrow x=\dfrac{-4+\sqrt{21}}{10}\)

\(\Leftrightarrow\dfrac{b^2+c^2-a^2}{2abc}+\dfrac{a^2+c^2-b^2}{2abc}+\dfrac{a^2+b^2-c^2}{2abc}=\dfrac{a}{bc}\)
\(\Leftrightarrow\dfrac{a^2+b^2+c^2}{2abc}=\dfrac{a}{bc}\)
\(\Leftrightarrow a^2+b^2+c^2=2a^2\)
\(\Leftrightarrow a^2=b^2+c^2\)
\(\Rightarrow\) Tam giác vuông tại A theo Pitago đảo


\(\Leftrightarrow\left\{{}\begin{matrix}x^3-x^2y-7\left(x-y\right)=x^2+y^2+2xy+4\\3x^2+y^2-8\left(x-y\right)+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x^2-7\right)\left(x-y\right)-x^2-2xy=y^2+4\\3x^2-8\left(x-y\right)=-y^2-4\end{matrix}\right.\)
Cộng vế:
\(\left(x^2-7\right)\left(x-y\right)-8\left(x-y\right)+2x^2-2xy=0\)
\(\Leftrightarrow\left(x^2-15\right)\left(x-y\right)+2x\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+2x-15\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=y\\x^2+2x-15=0\end{matrix}\right.\)
\(\Leftrightarrow...\)

\(f\left(x\right)=\left(m+1\right)x^2+mx+m\)
TH1: \(m+1=0\Leftrightarrow m=-1\Rightarrow f\left(x\right)>0,\forall x\in R\)
TH2: \(m+1\ne0\Leftrightarrow m\ne-1\)
Yêu cầu bài toán thỏa mãn khi \(\left\{{}\begin{matrix}\Delta=-3m^2-4m< 0\\m+1< 0\end{matrix}\right.\Leftrightarrow m< -\frac{4}{3}\)
Đ/s: \(m< -\frac{4}{3};m=-1\)

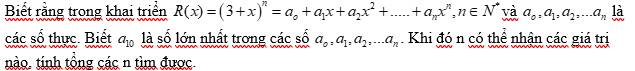








































Từ đề bài, ta thấy \(n\ge10\)
Với \(n=10\), xét khai triển \(R\left(n\right)=\left(3+x\right)^n\) \(\Rightarrow R\left(10\right)=\left(3+x\right)^{10}\) \(\sum\limits^{10}_{k=0}C^k_{10}3^{10-k}x^k\). Hệ số của số hạng chứa \(x^k\) là \(a_k=C^k_{10}.3^{10-k}\). Theo ycbt thì \(a_{10}\) là hệ số lớn nhất trong các \(a_i\left(i=\overline{0,10}\right)\) nên \(C^{10}_{10}.3^{10-10}=1\) là hệ số lớn nhất trong các hệ số. Nhưng \(a_5=C^5_{10}.3^5=61236>a_{10}\), mâu thuẫn.
Với \(n\ge11\), xét khai triển \(R\left(n\right)=\left(3+x\right)^n=\sum\limits^n_{k=0}C^k_n.3^{n-k}.x^k\). Hệ số của số hạng chứa \(x^k\) là \(a_k=C^k_n.3^{n-k}\). Do \(a_{10}\) là hệ số lớn nhất trong các số \(a_i\left(i=\overline{0,n}\right)\)nên \(\left\{{}\begin{matrix}a_{10}\ge a_9\\a_{10}\ge a_{11}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}C^{10}_n.3^{n-10}\ge C^9_n.3^{n-9}\\C^{10}_n.3^{n-10}\ge C^{11}_n.3^{n-11}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{n!}{10!\left(n-10\right)!}\ge\dfrac{n!}{9!\left(n-9\right)!}.3\\\dfrac{n!}{10!\left(n-10\right)!}.3\ge\dfrac{n!}{11!\left(n-11\right)!}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{10}\ge\dfrac{3}{n-9}\\\dfrac{3}{n-10}\ge\dfrac{1}{11}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}n\ge39\\n\le43\end{matrix}\right.\) \(\Leftrightarrow39\le n\le43\) (*)
(Ở đây mình chỉ so sánh hệ số \(a_{10}\) với \(a_9\) và \(a_{11}\) vì có xét với các \(a_i\) khác thì nó sẽ ra bất đẳng thức rộng hơn (*) nên mình quy về suy ra (*) luôn.)
Tổng các n là \(39+40+41+42+43=205\)
Mình còn thiếu \(n\in\left\{39;40;41;42;43\right\}\)