Cho hình thangABCD có số đo các gócA,B,C,D (theo đơn vị độ) lần lượt là\(3x;4x;x;2x\). Vậy x băng bao nhiêu độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 10 2014
tổng các góc trong tứ giác là:
A+B+C+D=360
mà A=3x;B=4x;C=x;D=2x)
suy ra 3x+4x+x+2x=360
x(3+4+1+2)=360
10x =360
x =360:10
x =36
TN
0
DL
13 tháng 9 2016
a) Gọi E, F lần lượt là giao điểm của AM và CD, BN và CD
Ta có : AB//CD (gt) => E = A1(so le trong)
Mà A1=A2(gt)
Nên A2 = E
Xét ΔADE cân tại D, có DM là p/giác nên DM đồng thời là trung tuyến
=>AM= EM
Chứng mih tương tự, ta được :
BN = FN
Xét hình thang ABEF có : AM=BN(cm trên)
BN=FN(cm trên)
Do đó MN là đường TB của HÌNH thang ABEF
=> MN=\(\frac{\text{EF}+AB}{2}\)
MN//AB//EF
Vậy MN// CD(đpcm)
b)Do ED= AD; BC=FC
Mà ED + DC + CF = EF
Nên AD + DC + BC = EF
Lại có MN\(\frac{\text{EF}+AB}{2}\) (CM trên)
Suy ra MN=\(\frac{AD+DC+BC+AB}{2}\) = \(\frac{a+b+c+d}{2}\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Do A, B, C, D theo thứ tự lập thành một cấp số cộng nên ta có:
B = A + d; C = A + 2d; D = A + 3d.
Mặt khác: A + B + C + D = 360°
⇔ A + A + d + A + 2d + A + 3d = 360°
⇔ 4A + 6d = 360°
⇔ 2A + 3d = 180°
Ta lại có: A + 2d = 5A ⇔ d = 2A
⇒ 8A = 180°
⇒ A = 22,5° và d = 45°
⇒ B = 67,5°, C = 112,5°, D = 157,5°.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
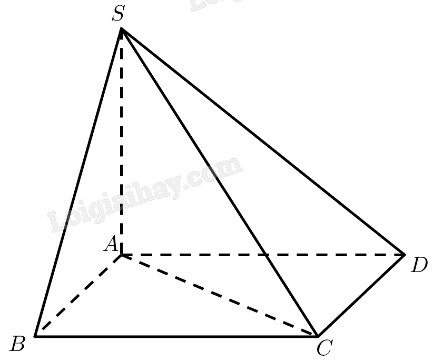
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{D}}\)
Vậy \(\widehat {BA{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,D} \right]\)
\(ABCD\) là hình vuông \( \Rightarrow \widehat {BA{\rm{D}}} = {90^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,D} \right]\) bằng \({90^ \circ }\).
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{C}}\)
Vậy \(\widehat {BA{\rm{C}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,C} \right]\)
\(ABCD\) là hình vuông \( \Rightarrow \widehat {BA{\rm{C}}} = {45^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,C} \right]\) bằng \({45^ \circ }\).
Tg ABCD có A +B + C + D = 360 độ
=> 3x + 4x + x + 2x = 360
=> 10x = 360
=> x = 36
VẬy x =36 độ