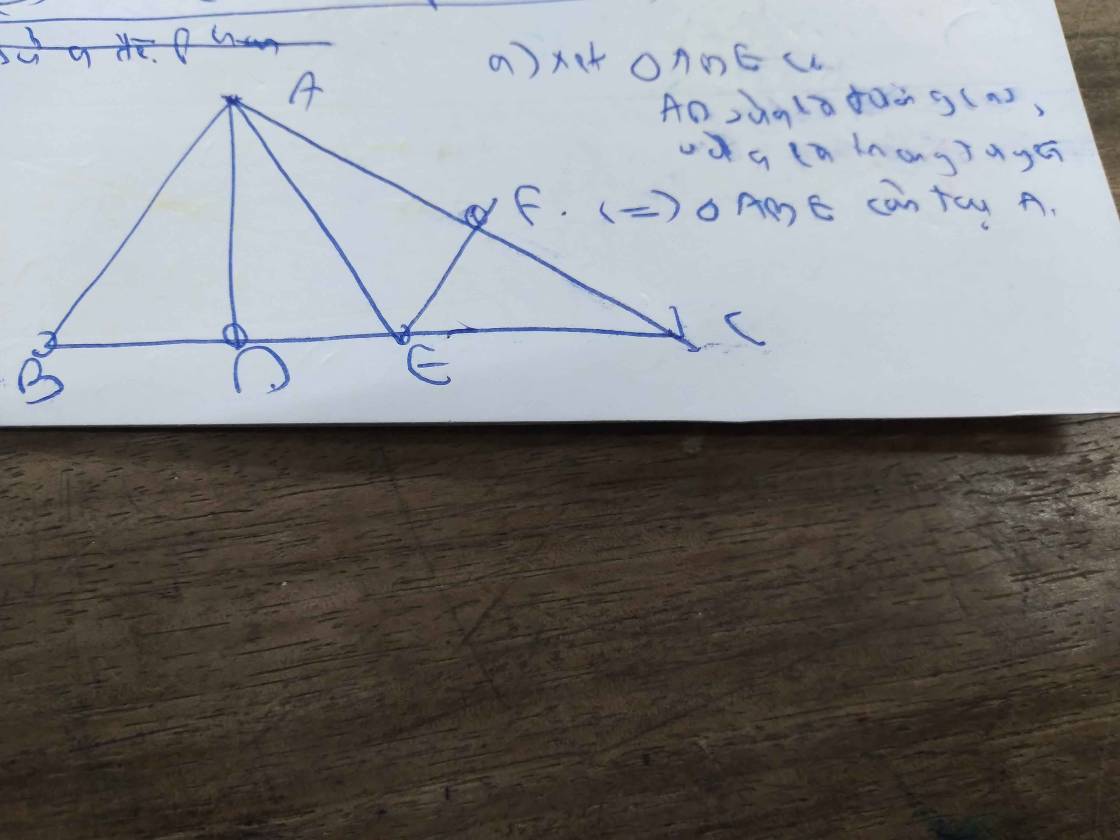
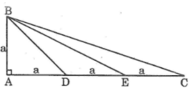
Cho tam giác nhọn ABC có AB < AC , đường cao AD . Trên đoạn DC lấy điểm E sao cho DB = DE .
a; Chứng minh tam giác ABE cân
b; Kẻ EF vuông góc với AC, (F thuộc AC), kẻ CK vuông góc với AE ,(K thuộc AE). Chứng minh rằng, ba đường thẳng AD, EF và CK đồng quy tại 1 điểm.


a.xét tam giác ADB và tam giác ADE có
DB=DE(gt)
góc ADB=góc ADE(vì AD là đg cao)
AD chung
=>tam giác ADB = tam giác ADE (c-g-c)
=>AB=AE(2 cạnh tương ứng bằng nhau)
=>tam giác ABE cân tại A (đpcm)
b.gọi H là giao điểm của AH,CK,EF
xét tam giác CHA có
FH vuông góc với AC,CD vuông góc với AH,AK vuông góc với CH
nên 3 đg AD,È,CK đồng quy tại điểm H (đpcm)
a: Xét ΔADB vuông tại D và ΔADE vuông tại D có
AD chung
DB=DE
Do đó: ΔADB=ΔADE
=>AB=AE
=>ΔABE cân tại A
b: Gọi H là giao điểm của CK và AD
Xét ΔAHC có
AK,CD là các đường cao
AK cắt CD tại E
Do đó: E là trực tâm của ΔAHC
=>HE⊥AC
mà EF⊥CA
và HE,EF có điểm chung là E
nên H,E,F thẳng hàng