\(x^2\left(x-1\right)-\left(x^2+1\right)\left(x+2\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
8 tháng 9 2021
x=2009x=2009
⇒x−1=2008(1)⇒x−1=2008(1)
Thay (1) vào A ta được:
A=x^2009−2008x^2008−2008x^2007−...−2008x+1
A=x^2009−(x−1)x^2008−...−(x−1)x+1
A=x^2009−x^2009+x^2008−...−x^2−x+1
A=−x+1
A=−2009+1
A=−2008
8 tháng 9 2021
\(x=2009\Leftrightarrow x-1=2008\\ \Leftrightarrow A=x^x-\left(x-1\right)x^{x-1}-\left(x-1\right)x^{x-2}-...-\left(x-1\right)x+1\\ \Leftrightarrow A=x^x-x^x+x^{x-1}-x^{x-1}+x^{x-2}-...-x^2-x+1\\ \Leftrightarrow A=1-x=1-2009=-2008\)
HT
2
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1 2024
\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)
T
12 tháng 1 2024
d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)
Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)
12 tháng 7 2023
12:
a: 40*7*25=8*5*7*25 chia hết cho 8
b: 32*19*28=8*4*19*28 chia hết cho 8
c: 4*35*2*39=8*35*39 chia hết cho 8
d: 14*27*4*15=2*4*7*27*15=8*7*25*15 chia hết cho 8
8 tháng 9 2021
\(e,\left(5+2\sqrt{6}\right)\left(49-20\sqrt{6}\right)\sqrt{5-2\sqrt{6}}\\ =\left(5+2\sqrt{6}\right)\left(\sqrt{3}-\sqrt{2}\right)\left(5-2\sqrt{6}\right)^2\\ =\left(5-2\sqrt{6}\right)\left(\sqrt{3}-\sqrt{2}\right)\\ =\left(\sqrt{3}-\sqrt{2}\right)^2\left(\sqrt{3}-\sqrt{2}\right)=\left(\sqrt{3}-\sqrt{2}\right)^3\)
\(f,\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}-\dfrac{1}{4}\sqrt{8}\right)\cdot3\sqrt{6}\\ =36-36\sqrt{2}+30\sqrt{3}-3\sqrt{3}=36-36\sqrt{2}+27\sqrt{3}\)
\(g,\left(2+\sqrt{3}-\sqrt{2}\right)\left(2-\sqrt{3}-\sqrt{2}\right)\left(3+\sqrt{2}\right)\sqrt{3-2\sqrt{2}}\\ =\left[\left(2-\sqrt{2}\right)^2-\left(\sqrt{3}\right)^2\right]\left(3+\sqrt{2}\right)\sqrt{\left(\sqrt{2}-1\right)^2}\\ =\left(3-4\sqrt{2}\right)\left(3+\sqrt{2}\right)\left(\sqrt{2}-1\right)\\ =\left(1-9\sqrt{2}\right)\left(\sqrt{2}-1\right)\\ =10\sqrt{2}-37\)
\(h,A=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\\ A^2=4+\sqrt{10+2\sqrt{5}}+4-\sqrt{10+2\sqrt{5}}+2\sqrt{\left(4+\sqrt{10+2\sqrt{5}}\right)\left(4-\sqrt{10+2\sqrt{5}}\right)}\\ A^2=8+2\sqrt{6-2\sqrt{5}}\\ A^2=8+2\left(\sqrt{5}-1\right)\\ A^2=6+2\sqrt{5}\\ A=\sqrt{6+2\sqrt{5}}=\sqrt{\left(\sqrt{5}+1\right)^2}=\sqrt{5}+1\)
8 tháng 9 2021
\(b,\sqrt{15-\sqrt{216}}+\sqrt{33-12\sqrt{6}}\\ =\sqrt{15-6\sqrt{6}}+\sqrt{\left(2\sqrt{6}-3\right)^2}\\ =\sqrt{\left(3-\sqrt{6}\right)^2}+2\sqrt{6}-3\\ =3-\sqrt{6}+2\sqrt{6}-3=\sqrt{6}\)
\(c,\sqrt{2-\sqrt{3}}\left(\sqrt{6}+\sqrt{2}\right)\\ =\sqrt{12-6\sqrt{3}}+\sqrt{4-2\sqrt{3}}\\ =\sqrt{\left(3-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}\\ =3-\sqrt{3}+\sqrt{3}-1=2\)
8 tháng 9 2021
c: \(\sqrt{2-\sqrt{3}}\cdot\left(\sqrt{6}+\sqrt{2}\right)\)
\(=\sqrt{4-2\sqrt{3}}\cdot\left(\sqrt{3}+1\right)\)
\(=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)\)
=3-1
=2
19 tháng 7 2021
a) Ta có: \(B=\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}\)
\(=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
b) Để B=16 thì \(4\sqrt{x+1}=16\)
\(\Leftrightarrow x+1=16\)
hay x=15
9 tháng 9 2021
\(C=\left(\dfrac{3}{x-1}+\dfrac{1}{\sqrt{x}+1}\right):\dfrac{1}{\sqrt{x}+1}\)
\(=\dfrac{3+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{1}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\)
27 tháng 9 2015
2P = 24.(5^2 + 1 )( 5^4 + 1 ) (5^8 + 1 )(5^16 + 1 )
2P = ( 5^2 - 1 )((5^2 + 1 )( 5^4 + 1 ) (5^ 8 + 1 )( 5^ 16 + 1)
2P = ( 5 ^ 4 - 1 )( 5 ^ 4 + 1 ) (5^8 + 1 )(5^16 + 1 )
2P = ( 5 ^8 - 1 )( 5^8 + 1 )( 5^16 + 1)
2P = ( 5 ^16 - 1 )( 5^16 + 1 )
2P = 5^32 - 1
=> P = \(\frac{5^{32}-1}{2}\)
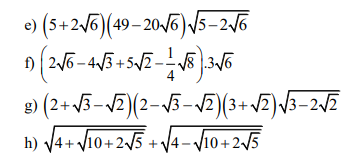
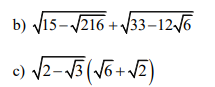
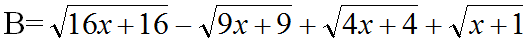
Ta có: \(x^2\left(x-1\right)-\left(x^2+1\right)\left(x+2\right)\)
\(=x^3-x^2-\left(x^3+2x^2+x+2\right)\)
\(=x^3-x^2-x^3-2x^2-x-2=-3x^2-x-2\)
\(x^2(x-1)-(x^2+1)(x+2)\)
\(=x^3-x^2-(x^3+2x^2+x+2)\)
\(=x^3-x^2-x^3-2x^2-x-2\)
\(=-3x^2-x-2\)
Đặt phương trình bằng \(0\), ta có:
\(-3x^2-x-2=0\rArr3x^2+x+2=0\)
Do đó: \(\Delta=1^2-4\cdot3\cdot2=1-24=-23<0\)
\(\rarr\) Phương trình vô nghiệm
Vậy phương trình vô nghiệm.