o
sos
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 3 2022
Đây là thấu kính hội tụ.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{12}=\dfrac{1}{d'}-\dfrac{1}{8}\Rightarrow d'=4,8cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{1}{h'}=\dfrac{8}{4,8}\Rightarrow h'=0,6cm\)
VT
27 tháng 8 2018
Đáp án: D
Tùy vào vị trí đặt vật mà ảnh của nó có thể lớn hơn, nhỏ hơn hoặc bằng vật, có thể cùng chiều hoặc ngược chiều với vật.
9 tháng 4 2022
Ảnh thật,ngược chiều và lớn hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{30}+\dfrac{1}{d'}\Rightarrow d'=60cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{3}{h'}=\dfrac{30}{60}\Rightarrow h'=6cm\)
VT
15 tháng 8 2019
Sơ đồ tạo ảnh:
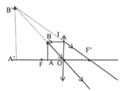
Nhìn qua thấu kính thấy 1 ảnh cùng chiều và cao gấp 3 lần vật nên k = 3
VT
29 tháng 6 2019
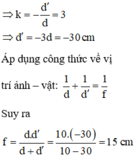
+ Vật thật qua thấu kính hội tụ cho ảnh cùng chiều với vật thì đó là ảnh ảo
VT
30 tháng 1 2018
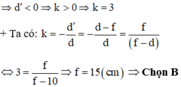
Đáp án: B
Giữa độ bội giác và tiêu cự f (đo bằng cm) có hệ thức: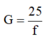 
LL
5 tháng 4 2021
F F' A B A' B' O
ảnh A'B' là ảnh thật, cùng chiều và lớn hơn vật
LL
5 tháng 4 2021
xétΔOAB và ΔOA'B'
\(\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\)⇒\(\dfrac{AB}{A'B'}=\dfrac{8}{OA'}\left(1\right)\)
xétΔOFI và ΔF'A'B'
\(\dfrac{OI}{A'B'}=\dfrac{12}{OF'+OA'}\)(2)
từ (1) và (2)⇒\(\dfrac{8}{OA'}=\dfrac{12}{12+OA'}\)
⇔8.(12+OA')=12.OA'
⇔96+8.OA'=12.OA'
⇔8.OA'-12.OA'=96
⇔-4.OA'=96
⇔OA'=-24 cm
thay OA'=-24 vào (1)
\(\dfrac{1}{A'B'}=\dfrac{8}{-24}\)⇒A'B'=\(-\dfrac{1}{3}\) cm