Thiết kế một chóa đèn có mặt cắt hình parabol với kích thước được cho trong hình sau:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
a) Vẽ lại hình vẽ như dưới đây
Ta có \(AB = 18,x = 3 \Rightarrow A(3;9)\)
Gọi phương trình parabol tổng quát \({y^2} = 2px\)
Thay tọa độ điểm A vào phương trình ta có: \({9^2} = 2p.3 \Rightarrow p = \frac{{27}}{2}\)
Vậy phương trình parabol trên hệ trục tọa độ vừa chọn là \({y^2} = 27x\)
b) Từ câu a) ta có: \(p = \frac{{27}}{2}\)
Suy ra tiêu điểm của parabol là \(F\left( {\frac{{27}}{4};0} \right)\)
Vậy để đèn chiếu được xa phải đặt bóng đèn cách đỉnh của chóa đèn \(\frac{{27}}{4}\) xentimét
CM
19 tháng 11 2018
Chọn B.
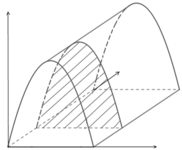
Phương pháp: Sử dụng tích phân.
Cách giải: Chọn hệ trục tọa độ như hình sao cho mặt trước của lều là mặt (Oxy), mặt đáy lều là mặt (Oyz).
CM
22 tháng 3 2017
Chọn đáp án C
Xét mặt cắt là một hình parabol, chọn hệ trục tọa độ như hình vẽ bên.
Phương trình parabol (P) có dạng y = a x 2 với a > 0 .
Ta thấy (P) đi qua các điểm (-4; 8) và (4; 8) nên a = 1 2 .
Suy ra phương trình parabol (P) là y = 1 2 x 2
Diện tích mặt cắt parabol của bồn nước cùng chính là diện tích của hình phẳng được giới hạn bởi các đường y = 1 2 x 2 và y = 8.
Diện tích đó là:
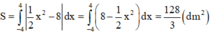
Do đó thể tích của bồn nước là: V = 2560 3 d m 3
CM
14 tháng 6 2017
Đáp án B.
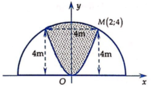Đặt hệ trục tọa độ như hình vẽ. Khi đó phương trình nửa đường tròn là
y
=
R
2
-
x
2
=
2
5
2
-
x
2
=
20
-
x
2
.
Phương trình parabol (P) có đỉnh là gốc O sẽ có dạng y = a x 2 . Mặt khác (P) qua điểm M(2;4) do đó 4 = a . - 2 2 ⇔ a = 1 .
Phần diện tích của hình phẳng giới hạn bởi (P) và nửa đường tròn (phần tô màu) là S 1 = ∫ - 2 2 20 - x 2 - x 2 d x ≈ 11 , 94 ( m 2 ) .
Phần diện tích trồng cỏ là: S t r o n g c o = 1 2 S h i n h t r o n - S 1 ≈ 19 , 47592654 m 2 .
Vậy số tiền cần có là S t r o n g c o × 100000 ≈ 1948000 (đồng).
Chóa đèn có hình dạng parabol nên phương trình mô phỏng chóa đèn có dạng \({y^2} = 2px\)
Gắn hệ tọa độ Oxy vào chóa đèn với gốc tọa độ tại đỉnh chóa đèn, suy ta phương trình đó đi qua điểm có tọa độ (3; 9)
Thay tọa độ điểm (3; 9) vào phương trình \({y^2} = 2px\), ta có \({9^2} = 2p.3 \Rightarrow p = \frac{{27}}{2}\)
Suy ra phương trình mô tả chóa đèn là \({y^2} = 27x\) với \(x \le 3\)
Hình ảnh mô phỏng chóa đèn có dạng như hình dưới: