Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Ta có: \(NP = 22,\;\widehat P = {180^o} - ({112^o} + {34^o}) = {34^o}\)
Áp dụng định lí sin, ta có:
\(\frac{{MN}}{{\sin P}} = \frac{{MP}}{{\sin N}} = \frac{{NP}}{{\sin M}}\)
Suy ra:
\(MP = \frac{{NP.\sin N}}{{\sin M}} = \frac{{22.\sin {{112}^o}}}{{\sin {{34}^o}}} \approx 36,48\)
\(MN = \frac{{NP.\sin P}}{{\sin M}} = \frac{{22.\sin {{34}^o}}}{{\sin {{34}^o}}} = 22.\)
QT
1
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
Mà \(AB = 14,AC = 18,\widehat A = {62^o}\)
\(\begin{array}{l} \Rightarrow B{C^2} = {18^2} + {14^2} - 2.18.14\cos {62^o} \approx 283,3863\\ \Leftrightarrow BC \approx 16,834\end{array}\)
Lại có: Từ định lí cosin ta suy ra:
\(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}};\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}}\)
\( \Rightarrow \left\{ \begin{array}{l}\cos B = \frac{{{{14}^2} + 16,{{834}^2} - {{18}^2}}}{{2.14.16,834}} \approx 0,3297\\\cos C = \frac{{{{18}^2} + 16,{{834}^2} - {{14}^2}}}{{2.18.16,834}} \approx 0,6788\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat B \approx {70^o}45'\\\widehat C \approx {47^o}15'\end{array} \right.\)
Vậy \(BC \approx 16,834;\widehat B \approx {70^o}45';\widehat C \approx {47^o}15'.\)
14 tháng 5 2020
A B C D E F 5 7 8 12 45 55
Giải
Vì\(\Delta ABC~\Delta DEF\) nên ta có:
\(\widehat{D}=\widehat{A}=45^o\)
\(\widehat{E}=\widehat{B}=55^o\)
\(\widehat{F}=\widehat{C}=\left(180^o-45^o-55^o\right)=80^o\)
Xét\(\Delta ABC~\Delta DEF\) có:
\(\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}=\frac{2}{3}\)
\(\Rightarrow DE=\frac{AB.3}{2}=7,5\)
\(DF=\frac{AC.3}{2}=10,5\)
#hoktot<3#
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
a) Vì tổng 3 góc trong tam giác là \({180^o}\)
Nên ta có :
\(\begin{array}{l} \Rightarrow \widehat {DEC} + \widehat {DCE} + \widehat {CDE} = {180^o}\\ \Rightarrow \widehat {DCE} = {180^o} - \widehat {DEC} - \widehat {CDE}\\ \Rightarrow \widehat {DCE} = {180^o} - {58^o} - {32^o} = {90^o}\end{array}\)
b) Theo đề bài ta có :
\(\begin{array}{l} \Rightarrow \widehat {HGF} + \widehat {GHF} + \widehat {GFH} = {180^o}\\ \Rightarrow \widehat {GFH} = {180^o} - \widehat {HGF} - \widehat {GHF}\\ \Rightarrow \widehat {GFH} = {180^o} - {68^o} - {42^o} = {70^o}\end{array}\)
c) Theo đề bài ta có :
\(\begin{array}{l} \Rightarrow \widehat {IJK} + \widehat {JKI} + \widehat {JIK} = {180^o}\\ \Rightarrow \widehat {JIK} = {180^o} - \widehat {IJK} - \widehat {JKI}\\ \Rightarrow \widehat {JIK} = {180^o} - {27^o} - {56^o} = {97^o}\end{array}\)
QT
1
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
a) Theo định lí về tổng số đo 3 góc trong tam giác ta có :
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat B = {180^o} - \widehat A - \widehat C = {180^o} - {72^o} - {44^o} = {64^o}\end{array}\)
b) Theo định lí về tổng số đo 3 góc trong tam giác ta có :
\(\begin{array}{l}\widehat D + \widehat E + \widehat F = {180^o}\\ \Rightarrow \widehat D = {180^o} - \widehat E - \widehat F = {180^o} - {59^o} - {31^o} = {90^o}\end{array}\)
c) Theo định lí về tổng số đo 3 góc trong tam giác ta có :
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat P = {180^o} - \widehat M - \widehat N = {180^o} - {120^o} - {33^o} = {27^o}\end{array}\)
CW
30 tháng 5 2016
Xét tam giác BOC có:
B1 + C1+ 135o = 180o
B1 +C1 = 45o
Ta có:
B= B1+ B2
C= C1+ C2
Và B +C +A = 180o
(B1+ B2)+ (C1+ C2) +A = 180o
2*B1 + 2*C1 +A = 180o
2* (B1+ C1) +A= 180o
2* 45o +A= 180o
90o +A= 180o
A= 90o
Ta có: B= 2C
và B +C +A = 180o
2C +C +90o =180o
3C = 90o
C = 30o
=> B= 2C = 2 * 30o= 60o
Mà tam giác ABC = tam giác DEF
=> A=D= 90o
E= B= 60o
C= F= 30o
QT
1
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Vì \(\Delta MNP\) cân tại M ( theo giả thiết )
\( \Rightarrow \widehat N = \widehat P = {70^o}\) ( 2 góc đáy của tam giác cân )
\( \Rightarrow \widehat M = {180^o} - {2.70^o} = {40^o}\)
b) Xét \(\Delta EFH\) cân tại E
Theo định lí về tổng 3 góc trong tam giác ta có
\( \Rightarrow \widehat E + \widehat F + \widehat H = {180^o}\)
Mà \(\widehat F = \widehat H\)( tính chất tam giác cân )
\( \Rightarrow \widehat F = \widehat H = {180^o} - \widehat E = ({180^o} - {70^o}):2 = {55^o}\)
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Ta có: \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\end{array} \right.\).
b) Xét tam giác \(DEF\) có:
\(\widehat D + \widehat E + \widehat F = 180^\circ \) (tổng ba góc trong một tam giác).
Ta có: \(\widehat D = 78^\circ ;\widehat E = 57^\circ \) thay số ta được
\(78^\circ + 57^\circ + \widehat F = 180^\circ \Rightarrow \widehat F = 180^\circ - 78^\circ - 57^\circ = 45^\circ \)
Ta có: \(\Delta DEF\backsim\Delta D'E'F' \Rightarrow \widehat D = \widehat {D'};\widehat E = \widehat {E'};\widehat F = \widehat {F'}\) (các góc tương ứng bằng nhau)
Do đó, \(\widehat D = \widehat {D'} = 78^\circ ;\widehat F = \widehat {F'} = 45^\circ \).
c) Ta có \(\Delta MNP\backsim\Delta M'N'P' \Rightarrow \frac{{MN}}{{M'N'}} = \frac{{MP}}{{M'P'}} = \frac{{NP}}{{N'P'}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Với \(MP = 10;NP = 6;M'N' = 15;N'P' = 12\) thay vào ta được:
\( \Rightarrow \left\{ \begin{array}{l}\frac{{MN}}{{15}} = \frac{1}{2}\\\frac{{10}}{{M'P'}} = \frac{1}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}MN = \frac{{15.1}}{2} = 7,5\\M'P' = \frac{{10.2}}{1} = 20\end{array} \right.\).
Vậy \(MN = 7,5;M'P' = 20\).
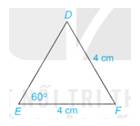
Cách 1: Vì tam giác DEF có DF=FE(=4cm) nên tam giác DEF cân tại F.
Mà \(\widehat E=60^0\)
Do đó, \(\Delta DEF \) đều. (Tam giác cân có 1 góc bằng \(60^0\))
\(\Rightarrow \widehat D = \widehat F=\widehat E=60^0\).
Cách 2: Xét tam giác DEF có DF=FE(=4cm) nên tam giác DEF cân tại F.
Suy ra \(\widehat E = \widehat D = {60^o}\) ( tính chất tam giác cân)
Áp dụng định lí tổng ba góc trong tam giác vào tam giác DEF, ta có:
\(\begin{array}{l}\widehat D + \widehat E + \widehat F = {180^o}\\ \Rightarrow {60^o} + {60^o} + \widehat F = {180^o}\\ \Rightarrow \widehat F = {60^o}\end{array}\)