cho lăng trụ đứng ABC. A'B'C' có đáy là tam giác ABC vuông tại A có AB=6, BC=10, AA'=5. Tính thể tích hình lăng trụ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 9
Sửa đề: A'A=12cm
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=25^2-15^2=625-225=400=20^2\)
=>AC=20(cm)
Chu vi đáy là:
15+20+25=40+20=60(cm)
Diện tích xung quanh của lăng trụ là:
\(60\cdot12=720\left(\operatorname{cm}^2\right)\)
CM
9 tháng 12 2019
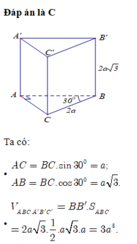
Ta có:
• A C = B C . sin 30 0 = a ; A B = B C . cos 30 0 = a 3 .
• V A B C . A ' B ' C ' = B B ' . S A B C = 2 a 3 . 1 2 . a 3 . a = 3 a 3 .
CM
20 tháng 10 2018
Đáp án B.
Hình trụ ngoại tiếp hình lăng trụ ABC.A’B’C’ có chiều cao AA’; tâm của đáy là trung điểm của AC nên
CM
9 tháng 10 2019
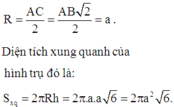
Đáp án C
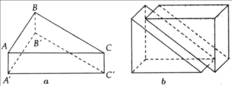
Thể tích khối lăng trụ là: V = A A ' . S A B C = a . 1 2 a .2 a = a 3
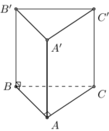
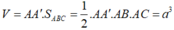
\(AC=\sqrt{10^2-6^2}=8\)
S đáy=1/2*6*8=3*8=24
V=24*5=120