tìm x thuộc z biết x + (x+1) + (x+2) + ... + 2023 + 2024 = 2024
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 9
a: \(8x\left(2023+x\right)-8x\left(x+2024\right)=56\)
=>\(8x\left(x+2023-x-2024\right)=56\)
=>-8x=56
=>\(x=\frac{56}{-8}=-7\) (nhận)
b: \(5-2025x=9-2026\left(x-1\right)\)
=>-2025x+5=9-2026x+2026
=>-2025x+5=-2026x+2035
=>x=2035-5=2030(nhận)
c: \(\left(-12\right)^2\cdot x=56+10\cdot13x\)
=>144x=56+130x
=>14x=56
=>x=4(nhận)
d: -(x-32+11)=(21-33-x+7)
=>-(x-21)=(-x-5)
=>-x+21=-x-5
=>21=-5(vô lý)
=>x∈∅
e: \(-2\left(x+6\right)+6\left(x+10\right)=8\)
=>-2x-12+6x+60=8
=>4x+52=8
=>4x=8-52=-44
=>\(x=-\frac{44}{4}=-11\) (nhận)
25 tháng 12 2023
a: \(\left|a-2b+3\right|^{2023}>=0\forall a,b\)
\(\left(b-1\right)^{2024}>=0\forall b\)
Do đó: \(\left|a-2b+3\right|^{2023}+\left(b-1\right)^{2024}>=0\forall a,b\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}a-2b+3=0\\b-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=1\\a=2b-3=2\cdot1-3=-1\end{matrix}\right.\)
Thay a=-1 và b=1 vào P, ta được:
\(P=\left(-1\right)^{2023}\cdot1^{2024}+2024=2024-1=2023\)
NM
tìm giá trị lớn nhất của P = \(\dfrac{|x-2022|-|x-2023|+|x-2024|+2022}{|x-2022|+|x-2023|+|x-2024|}\)
0
AH
Akai Haruma
Giáo viên
15 tháng 7 2023
Lời giải:
Ta có:
$(x+y+z)(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})=2023.\frac{2024}{2023}$
$\Leftrightarrow 1+\frac{x}{y}+\frac{x}{z}+\frac{y}{x}+1+\frac{y}{z}+\frac{z}{x}+\frac{z}{y}+1=2024$
$\Leftrightarrow 3+\frac{x+z}{y}+\frac{y+z}{x}+\frac{x+y}{z}=2024$
$\Leftrightarrow 3+B=2024$
$\Leftrightarrow B=2021$
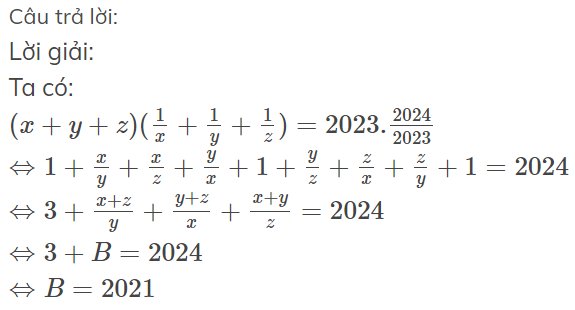
\(x+\left(x+1\right)+\left(x+2\right)+...+2023+2024=2024\)
\(\Rightarrow2023x+4090506=2024-2024-20232023\)
\(\Rightarrow x+4090506=-2023\)
\(\Rightarrow2023x=-2023-4090506\)
\(\Rightarrow2023x=-4092529\)
\(\Rightarrow x=-2023\).
1011