Cho 4 điểm em hãy nối các điểm trong hình bên để có 5 cặp đoạn thẳng vuông góc với nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 3 2019
Có hai trường hợp:
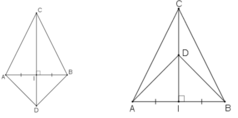
+ ΔAIC = ΔBIC (c.g.c) vì:
AI = IB (gt)
∠AIC = ∠BIC = 90o
CI chung.
+ ΔAID = ΔBID(c.g.c) vì:
AI = ID (gt)
∠AID = ∠BID = 90o
DI chung.
+ ΔACD = ΔBCD(c.c.c) vì:
AC = BC (Lấy từ ΔAIC = ΔBIC)
AD = BD (Lấy từ ΔAID = ΔBID)
CD chung
R
18 tháng 12 2018
Xét tam giác ACI và tam giác BCI , có
CI là cạnh chung
AC = BC
AI= BI
=> tam giác ACI = tam giác BCI
Xét tam giác ACD và tam giác BCD , có
CD là cạnh chung
AD = BD
AC =BC
=> tam giác ACD = tam giác BCD
Xét tam giác ADI và tam giác BDI , có
DI là cạnh chung
AD = BD
AI = BI
=> tam giác ADI = tam giác BDI
ok 3 cặp nha
BN
18 tháng 12 2018
A B I O C D
Vì ID là tia phân giác của đoạn thẳng AB
=> AD = BD
AI = BI
Xét ∆ AID và ∆ BID có :
AD = BD ( cmt )
ID là cạnh chung
AI = BI ( cmt )
=> ∆ AID = ∆ BID ( c.c.c )
Xét ∆ ACI và ∆ IBC có :
AC = BC ( theo hình vẽ )
IC là cạnh chung
AI = BI ( cmt )
=> ∆ ACI = ∆ IBC ( c.c.c )
Xét ∆ ACD và ∆ BCD có :
AD = BD ( cmt )
CD là cạnh chung
AC = BC ( cmt )
=> ∆ ACD = ∆ BCD ( c.c.c )
Vậy có 3 cặp tam giác bằng nhau
Cũng có thể chứng minh theo cách cạnh - góc - cạnh nhưng mình thích cạnh - cạnh - cạnh hơn :3
CQ
28 tháng 6
Để giải bài toán này, ta cần hiểu rõ các điều kiện:
- Có một hình vuông, tức là 4 đỉnh.
- Có thêm 10 điểm phân biệt bên trong (tổng cộng có 14 điểm: 4 đỉnh + 10 điểm trong).
- Không có 3 điểm nào thẳng hàng.
- Nối các điểm với nhau bằng các đoạn thẳng, sao cho không có hai đoạn nào cắt nhau, chỉ được phép cắt ở đầu mút.
- Hỏi: Số tam giác tối đa có thể tạo thành là bao nhiêu?
🔍 Phân tích:
Bài toán này liên quan đến đồ thị phẳng (planar graph), nơi mà ta nối các điểm lại bằng đoạn thẳng mà không có đoạn nào cắt nhau (trừ tại đầu mút), và đếm số tam giác (số mặt tam giác) có thể tạo ra tối đa.
🎯 Mục tiêu:
Tìm số tam giác tối đa tạo được trong một đồ thị phẳng có 14 điểm (nút) và không có cạnh nào cắt nhau (trừ ở đầu mút).
🔶 Áp dụng công thức Euler cho đồ thị phẳng:
Đồ thị phẳng không có giao điểm (chỉ giao nhau ở đầu mút), thỏa mãn:
\(V - E + F = 2\)
Trong đó:
- \(V\): số đỉnh = 14
- \(E\): số cạnh
- \(F\): số mặt (bao gồm mặt ngoài)
Giả sử tất cả mặt bên trong là tam giác ⇒ mỗi mặt có 3 cạnh. Mỗi cạnh thuộc về 2 mặt ⇒ ta có:
\(3 \left(\right. F - 1 \left.\right) = 2 E\)
(tức là bỏ 1 mặt ngoài, còn lại đều là tam giác)
Kết hợp công thức Euler và đếm cạnh:
\(V - E + F = 2 \Rightarrow 14 - E + F = 2 \Rightarrow F = E - 12\)
Thay vào \(3 \left(\right. F - 1 \left.\right) = 2 E\):
\(3 \left(\right. E - 13 \left.\right) = 2 E \Rightarrow 3 E - 39 = 2 E \Rightarrow E = 39\)
⇒ \(F = 39 - 12 = 27\)
→ Số tam giác tối đa là \(F - 1 = 26\)
✅ Kết luận:
Số tam giác tối đa tạo ra được là:26
13 tháng 11 2016
Nguyễn Huy Thắng
soyeon_Tiểubàng giải
Nguyễn Đình Dũng
Nguyễn Huy Tú
Trần Quỳnh Mai
Nguyễn Anh Duy
Silver bullet
Trần Minh Hưng
Hoàng Lê Bảo Ngọc
Trương Hồng Hạnh
Trần Việt Linh
Võ Đông Anh Tuấn
Phương An
Lê Nguyên Hạo
Nguyễn Phương HÀ