Xét tính tăng, giảm của dãy số (un) có số hạng tổng quát un = 2n - 3n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 11 2021
Dãy đã cho hiển nhiên là dãy dương
Ta sẽ chứng minh dãy đã cho bị chặn trên bởi 2 hay \(u_n\le2\) với mọi n
- Với \(n=1\Rightarrow u_1=\sqrt{2}< 2\) (đúng)
- Giả sử điều đó đúng với \(n=k\ge1\) hay \(u_k\le2\)
- Ta cần chứng minh với \(n=k+1\) cũng đúng
Hay \(u_{k+1}\le2\)
Ta có: \(u_{k+1}=\sqrt{2+u_k}\le\sqrt{2+2}=2\) (đpcm)
Vậy \(u_n\le2\)
Đặt \(v_n=\dfrac{1}{2}u_n\Rightarrow0< v_n\le1\) và \(\left\{{}\begin{matrix}v_1=\dfrac{\sqrt{2}}{2}=cos\left(\dfrac{\pi}{4}\right)\\2v_{n+1}=\sqrt{2+2v_n}\end{matrix}\right.\)
\(\Rightarrow4v_{n+1}^2=2+2v_n\Rightarrow v_n=2v_{n+1}^2-1\)
Do \(0< v_n\le1\) , đặt \(v_n=cos\left(x_n\right)\) với \(x_n\in\left(0;\pi\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{\pi}{4}\\cos\left(x_n\right)=2cos^2\left(x_{n+1}\right)-1=cos\left(2x_{n+1}\right)\end{matrix}\right.\)
\(\Rightarrow x_n=2x_{n+1}\Rightarrow x_{n+1}=\dfrac{1}{2}x_n\)
\(\Rightarrow x_n\) là CSN với công bội \(\dfrac{1}{2}\)
\(\Rightarrow x_n=\dfrac{\pi}{4}.\left(\dfrac{1}{2}\right)^{n-1}=\dfrac{\pi}{2^{n+1}}\)
\(\Rightarrow v_n=cos\left(x_n\right)=cos\left(\dfrac{\pi}{2^{n+1}}\right)\)
\(\Rightarrow u_n=2v_n=2cos\left(\dfrac{\pi}{2^{n+1}}\right)\)
Dãy \(\dfrac{\pi}{2^{n+1}}\) giảm và thuộc \(\left(0;\dfrac{\pi}{2}\right)\) nên \(cos\left(\dfrac{\pi}{2^{n+1}}\right)\) tăng
Do đó dãy số đã cho là dãy tăng.
P/s: đây là cách làm hoàn chỉnh có thứ tự (nhược điểm là rất dài). Có 1 cách khác đơn giản hơn là bằng 1 phép màu nào đó ngay từ đầu bạn đưa ra ngay dự đoán công thức tổng quát của dãy số là \(2cos\left(\dfrac{\pi}{2^{n+1}}\right)\) rồi chứng minh nó bằng quy nạp cũng được. Như vậy sẽ rất ngắn, cả bài chỉ 4-5 dòng nhưng lời giải hơi đột ngột
CM
28 tháng 3 2018
Giả sử u n = 167 84 ⇔ 2 n + 1 n + 2 = 167 84 ⇔ 84 ( 2 n + 1 ) = 167 ( n + 2 )
⇔ 168 n + 84 = 167 n + 334 ⇔ n = 250
Vậy 167 84 là số hạng thứ 250 của dãy số ( u n ) .
Chọn đáp án C.
15 tháng 10 2023
1:
a: \(u_2=2\cdot1+3=5;u_3=2\cdot5+3=13;u_4=2\cdot13+3=29;\)
\(u_5=2\cdot29+3=61\)
b: \(u_2=u_1+2^2\)
\(u_3=u_2+2^3\)
\(u_4=u_3+2^4\)
\(u_5=u_4+2^5\)
Do đó: \(u_n=u_{n-1}+2^n\)
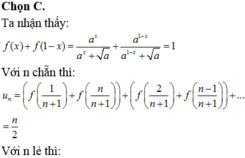
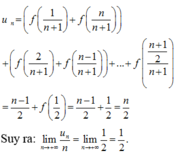
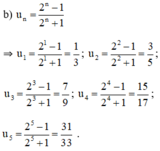
Ta sẽ chứng minh dãy này giảm theo quy nạp.
Với n = 1 ta có u1 = -1
Với n = 2 ta có u2 = -5
=> u1 > u2
Giả sử dãy trên đúng với uk > uk+1 tức 2k - 3k > 2(k + 1) - 3k + 1 <=> 2k - 2(k + 1) > 3k - 3k+1
Ta cần chứng minh dãy cũng đúng với uk+1 > uk+2
Hay 2(k + 1) - 3k+1 > 2(k + 2) - 3k+2
<=> 2k - 3.3k > 2(k + 1) - 3.3k+1
<=> 2k - 2(k + 1) > 3.(3k - 3k+1)
Thật vậy: Với k nguyên dương ta luôn có 3k - 3k+1 < 0 và 3 > 1 nên 3(3k - 3k+1) < 3k - 3k+1
Lại có 2k - 2(k + 1) > 3k - 3k+1 => 2k - 2(k + 1) > 3.(3k - 3k+1) (đpcm)
Vậy dãy un trên là dãy giảm