Ai giúp em với an,em cần gấp r ,vẽ thêm hình giúp e ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
T
1
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 12 2022
Mình không nhìn thấy câu hỏi, giờ mới thấy bạn ạ
Do mở rộng cạnh của thửa đất về cả bốn phía nên thửa đất mới sau khi mở rộng cũng là hình vuông. mỗi cạnh của thửa đất lúc sau đã tăng :
0,5 x 2 = 1 (m)
Gọi cạnh hình vuông lúc đầu là x đk x > 0
Thì cạnh hình vuông lúc sau là : x + 1
theo bài ra ta có : (x + 1)( x + 1) - x2 = 20
x2 + x + x + 1 - x2 = 20
2x = 20 -1
2x = 19
x = 19: 2
x = 9,5
Kết luận cạnh hình vuông lúc đầu là 9,5 m
VT
1
21 tháng 10 2021
Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\)
hay MN//BP và MN=BP
Xét tứ giác BMNP có
MN//BP
MN=BP
Do đó: BMNP là hình bình hành
A
1
T
2
TN
0
A
1
29 tháng 1 2024
a:
Gọi O là trung điểm của AD
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó:ΔACD vuông tại C
Xét tứ giác EFDC có \(\widehat{EFD}+\widehat{ECD}=90^0+90^0=180^0\)
nên EFDC là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{BCA}\) là góc nội tiếp chắn cung BA
\(\widehat{BDA}\) là góc nội tiếp chắn cung BA
Do đó: \(\widehat{BCA}=\widehat{BDA}\)
mà \(\widehat{BDA}=\widehat{ACF}\)(ECDF là tứ giác nội tiếp)
nên \(\widehat{BCA}=\widehat{ACF}\)
=>CA là phân giác của góc BCF
QH
3
KV
25 tháng 8
Bài 1
a) Do ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB và AB = AC
Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠ABC : 2
Do CE là tia phân giác của ∠ACB (gt)
⇒ ∠ACE = ∠ACB : 2
Mà ∠ABC = ∠ACB (cmt)
⇒ ∠ABD = ∠ACE
Xét ∆ABD và ∆ACE có:
∠ABD = ∠ACE (cmt)
AB = AC (cmt)
∠A chung
⇒ ∆ABD = ∆ACE (g-c-g)
⇒ AD = AE (hai cạnh tương ứng)
⇒ ∆ADE cân tại A
⇒ ∠AED = (180⁰ - ∠DAE) : 2 = (180⁰ - ∠BAC) : 2 (1)
Do ∆ABC cân tại A (gt)
⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (2)
Từ (1) và (2) ⇒ ∠AED = ∠ABC
Mà ∠AED và ∠ABC là hai góc đồng vị
⇒ ED // BC
⇒ BEDC là hình thang
Lại có ∠ABC = ∠ACB (cmt)
⇒ ∠EBC = ∠DCB
⇒ BEDC là hình thang cân
b) Do ∠C = 50⁰ (gt)
⇒ ∠DCB = ∠EBC = 50⁰
⇒ ∠AED = ∠EBC = 50⁰
Mà ∠AED + ∠BED = 180⁰ (kề bù)
⇒ ∠BED = 180⁰ - ∠AED = 180⁰ - 50⁰ = 130⁰
⇒ ∠CDE = ∠BED = 130⁰
25 tháng 8
Bài 4:
a: Xét ΔABC có \(\frac{AD}{AB}=\frac{AE}{AC}\)
nên DE//BC
Xét tứ giác BDEC có DE//BC và \(\hat{DBC}=\hat{ECB}\) (ΔABC cân tại A)
nên BDEC là hình thang cân
b: BD=DE
=>ΔDEB cân tại D
=>\(\hat{DEB}=\hat{DBE}\)
mà \(\hat{DEB}=\hat{EBC}\) (hai góc so le trong, DE//BC)
nên \(\hat{DBE}=\hat{CBE}\)
=>\(\hat{ABE}=\hat{CBE}\)
=>BE là phân giác của góc ABC
=>E là chân đường phân giác kẻ từ B xuống AC của ΔABC
Ta có: ED=EC
=>ΔEDC cân tại E
=>\(\hat{EDC}=\hat{ECD}\)
mà \(\hat{EDC}=\hat{DCB}\) (hai góc so le trong, ED//BC)
nên \(\hat{ECD}=\hat{BCD}\)
=>\(\hat{ACD}=\hat{BCD}\)
=>CD là phân giác của góc ACB
=>D là chân đường phân giác kẻ từ C xuống AB của ΔABC
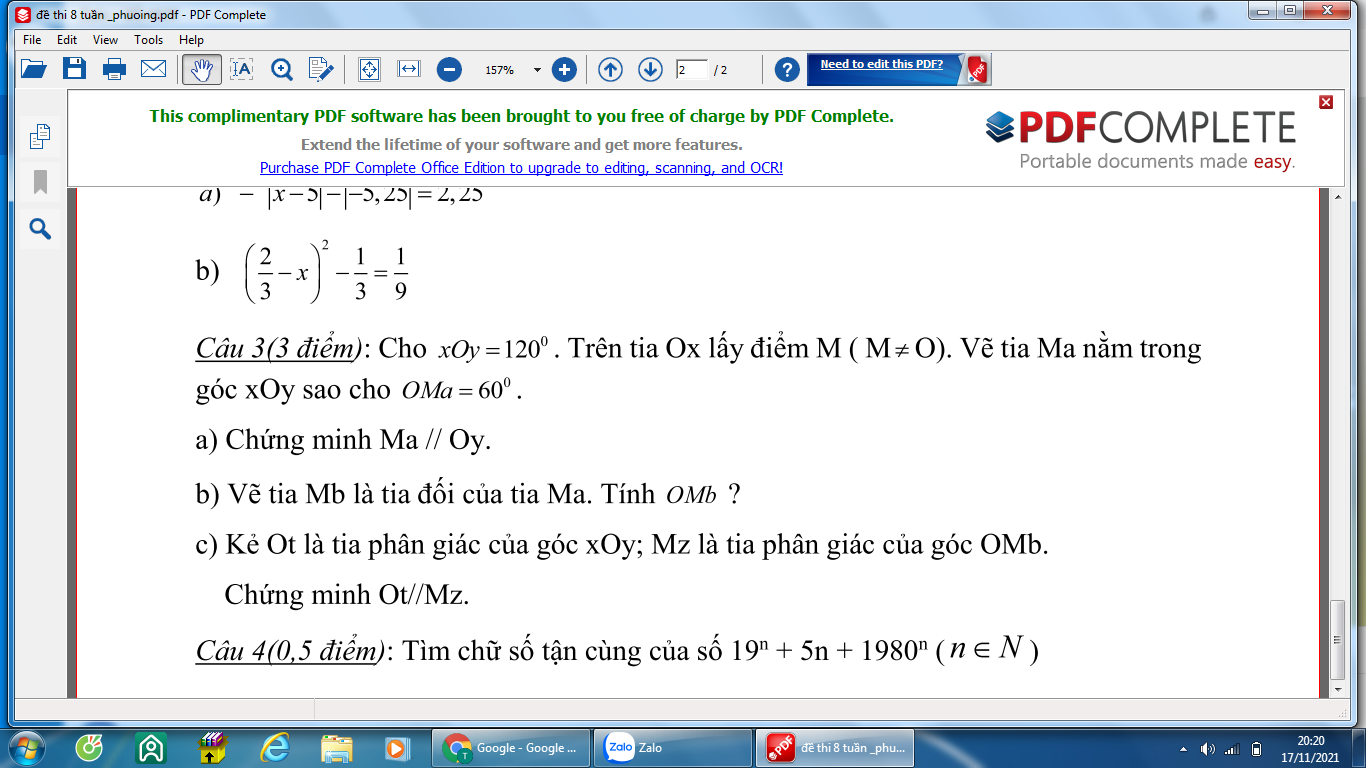
Bài 3:
a: ΔCAD vuông tại C
=>\(\hat{CAD}+\hat{CDA}=90^0\)
=>\(\hat{CAD}=90^0-60^0=30^0\)
AC là phân giác của góc BAD
=>\(\hat{BAD}=2\cdot\hat{CAD}=2\cdot30^0=60^0\)
Xét hình thang ADCB có \(\hat{BAD}=\hat{CDA}\left(=60^0\right)\)
nên ADCB là hình thang cân
b: Qua B, kẻ BK⊥AD tại K
Qua C, kẻ CH⊥AD tại H
=>BK//CH
Xét ΔBKA vuông tại K và ΔCHD vuông tại H có
BA=CD
\(\hat{BAK}=\hat{CDH}\)
Do đó: ΔBKA=ΔCHD
=>BK=CH và AK=HD
Gọi M là trung điểm của CD
Trên tia đối của tia MH, lấy E sao cho MH=ME
=>M là trung điểm của HE
Xét tứ giác CHDE có
M là trung điểm chung của CD và HE
=>CHDE là hình bình hành
Hình bình hành CHDE có \(\hat{CHD}=90^0\)
nên CHDE là hình chữ nhật
=>CD=HE
mà \(CM=MD=\frac{CD}{2};MH=ME=\frac{HE}{2}\)
nên \(CM=MD=MH=ME\)
Xét ΔDMH có MH=MD và \(\hat{MDH}=60^0\)
nên ΔMDH đều
=>DH=MD=CD/2
Ta có: BC//AD
=>\(\hat{BCA}=\hat{CAD}\) (hai góc so le trong)
mà \(\hat{CAD}=\hat{BAC}\)
nên \(\hat{BCA}=\hat{BAC}\)
=>BA=BC
mà BA=CD
nên BA=BC=CD
AK=HD
mà \(HD=\frac{CD}{2}\)
nên \(AK=HD=\frac{CD}{2}\)
Xét tứ giác BCHK có
BC//HK
BK//CH
Do đó: BCHK là hình bình hành
=>BC=HK
=>\(HK=CD\)
AD=AK+KH+HD
\(=\frac{CD}{2}+CD+\frac{CD}{2}=2CD\)
Chu vi hình thang ABCD là:
AB+BC+CD+DA=20
=>CD+CD+CD+2CD=20
=>5CD=20
=>CD=4(cm)
=>\(AD=2\cdot4=8\left(\operatorname{cm}\right)\)
Bài 2:
a: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
=>\(\hat{ABD}=\hat{BAC}\)
=>\(\hat{OAB}=\hat{OBA}\)
=>OA=OB
ta có: OA+OC=AC
OB+OD=BD
mà OA=OB và AC=BD
nên OC=OD
b: Xét ΔEDC có \(\hat{EDC}=\hat{ECD}\)
nên ΔEDC cân tại E
=>ED=EC
Ta có: EA+AD=ED
EB+BC=EC
mà ED=EC và AD=BC
nên EA=EB
Ta có: EA=EB
=>E nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
từ (1),(2) suy ra EO là đường trung trực của AB
Ta có: EC=ED
=>E nằm trên đường trung trực của CD(3)
ta có: OC=OD
=>O nằm trên đường trung trực của CD(4)
Từ (3),(4) suy ra EO là đường trung trực của CD
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED