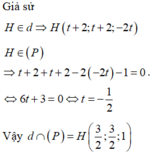Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và mặt phẳng Gọi d’ là hình chiếu của đường thẳng d lên mặt phẳng (P), vectơ chỉ phương của đường thẳng d’ là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn B

Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Chọn A
Tìm giao điểm I từ hệ phương trình đường thẳng d và mặt phẳng (P). Viết phương trình đường thẳng IM. Gọi tọa độ điểm M theo tham số của đường thẳng IM rồi xác định tham số đó từ phương trình I M = 4 14

Phương trình \(d_1\) : \(\dfrac{x-1}{1}=\dfrac{y-2}{-1}=\dfrac{z-3}{-1}\) dạng tham số: \(\left\{{}\begin{matrix}x=1+t\\t=2-t\\z=3-t\end{matrix}\right.\)
Gọi A là giao điểm d1 và (P), tọa độ A thỏa mãn:
\(3-t-1=0\Rightarrow t=2\Rightarrow A\left(3;0;1\right)\)
\(\overrightarrow{n_P}=\left(0;0;1\right)\) ; \(\overrightarrow{n_Q}=\left(1;1;1\right)\)
\(\overrightarrow{u_{\Delta}}=\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(-1;1;0\right)\)
\(\left[\overrightarrow{u_{\Delta}};\overrightarrow{n_P}\right]=\left(1;1;0\right)\)
Phương trình d: \(\left\{{}\begin{matrix}x=3+t\\y=t\\z=1\end{matrix}\right.\)

Đáp án B
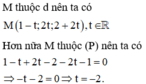
Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Đáp án B.
Ta có: Hai vector chỉ phương của hai đường thẳng là cùng phương nên hai đường thẳng luôn đồng phẳng.
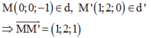
Vector chỉ phương của đường thẳng d là u → = ( 1 ; - 2 ; - 1 )
Vector pháp tuyến của mặt phẳng
![]()
Phương trình mặt phẳng
![]()

Đáp án C
HD: Gọi H(1+2t;-1+t;2-t) là hình chiếu của A trên d
![]()
![]()
Suy ra H(3;0;1), phương trình đường thẳng AH là
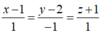
![]()