Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng cắt ba trục tọa độ tại ba điểm A(2;0;0), B(0;3;0), C(0;0;1) Phương trình của α là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương trình theo đoạn chắn của mặt phẳng α là x 2 + y 3 + z 1 = 1

Đáp án D
Phương trình theo đoạn chắn của mặt phẳng (α) là x 2 + y 3 + z 1 = 1


Mặt phẳng
α
chứa A và trục Oy nên có một VTPT là ![]()
Đường thẳng
∆
là giao tuyến của
α
và
β
nên có VTCP ![]()
Theo giả thiết, ta có
u
∆
→
cùng phương với ![]()
Suy ra 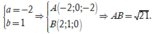
Chọn C.

Chọn B
Gọi A(a;0;0), B(0;b;0), C(0;0;c). Ta có phương trình mặt phẳng (P) là: ![]()
Gọi H là hình chiếu của O lên (P). Ta có: d(O, (P)) = OH ≤ OM
Do đó max d(O, (P)) = OM khi và chỉ khi (P) qua M nhận ![]() làm VTPT.
làm VTPT.
Do đó (P) có phương trình:
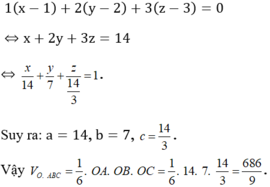







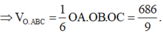
Chọn D