Trong không gian với hệ trục tọa độ Oxyz, gọi (P) là mặt phẳng đi qua hai điểm A(1;1;1), B(0;1;2) và khoảng cách từ C(2;-1;1) đến mặt phẳng (P) bằng . Giả sử phương trình mặt phẳng (P) có dạng ax +by +cz +2 =0. Tính giá trị abc.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Hình chiếu của A(1 ;2 ;3) lên trục Ox là M(1;0;0)
Hình chiếu của A(1 ;2 ;3) lên trục Oy là N(0;2;0)
Hình chiếu của A(1 ;2 ;3) lên trục Ox là P(0;0;3)
Phương trình mặt phẳng (P) cần tìm là:
![]()

Chọn B
Gọi A(a;0;0), B(0;b;0), C(0;0;c). Ta có phương trình mặt phẳng (P) là: ![]()
Gọi H là hình chiếu của O lên (P). Ta có: d(O, (P)) = OH ≤ OM
Do đó max d(O, (P)) = OM khi và chỉ khi (P) qua M nhận ![]() làm VTPT.
làm VTPT.
Do đó (P) có phương trình:
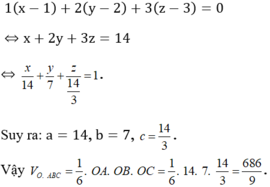

Đáp án B
Gọi H là hình chiếu của O trên (P) => d(O;(P)) = OH ≤ OM
Dấu bằng xảy ra khi và chỉ khi H ≡ M => n P → = (1;2;3) => (P): x + 2y + 3z - 14 = 0
Mặt phẳng (P) cắt các trục tọa độ lần lượt tại A(14;0;0); B(0;7;0); C(0;0; 14 3 )
Vậy thể tích khối chóp OABC là 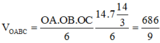


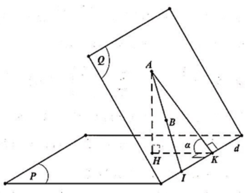



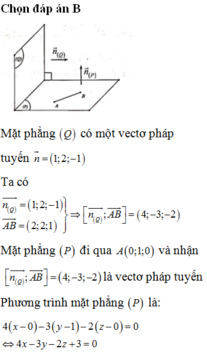

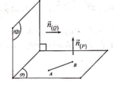
Chọn đáp án C.