Cho Tìm căn bậc hai dạng lượng giác của z:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1, \(sin\left(x+\dfrac{\pi}{6}\right)+cos\left(x+\dfrac{\pi}{6}\right)=\dfrac{\sqrt{6}}{2}\)
⇔ \(\dfrac{\sqrt{2}}{2}sin\left(x+\dfrac{\pi}{6}\right)+\dfrac{\sqrt{2}}{2}cos\left(x+\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}\)
⇔ \(sin\left(x+\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)=sin\dfrac{\pi}{4}\)
2, \(\left(\sqrt{3}-1\right)sinx+\left(\sqrt{3}+1\right)cosx=1-\sqrt{3}\)
⇔ \(\dfrac{\left(\sqrt{3}-1\right)}{2\sqrt{2}}sinx+\dfrac{\left(\sqrt{3}+1\right)}{2\sqrt{2}}cosx=\dfrac{1-\sqrt{3}}{2\sqrt{2}}\)
⇔ sinx . si

1.
\(\frac{\pi}{2}< x< \pi\\ \Rightarrow cosx< 0,sinx>0,cotx< 0\)
\(cotx=\frac{1}{tanx}=\frac{-1}{3}\)
\(1+tan^2x=\frac{1}{cos^2x}\\ \Rightarrow cosx=\sqrt{\frac{1}{1+tan^2}}=\sqrt{\frac{1}{1+9}}=-\frac{\sqrt{10}}{10}\)
\(sinx=\sqrt{1-cos^2x}=\sqrt{1-\frac{10}{100}}=\frac{3\sqrt{10}}{10}\)

Đề như vậy hả bạn: \(\frac{3cosx+4sinx+6}{3cosx+4sinx+1}=2\)

Các số có căn bậc hai:
a = 0 c = 1 d = 16 + 9
e = 32 + 42 h = (2-11)2 i = (-5)2
l = √16 m = 34 n = 52 - 32
Căn bậc hai không âm của các số đó là:
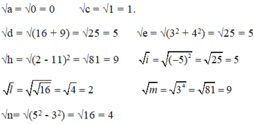

Chọn D.
Ta có phương trình đã cho tương đương với phương trình:
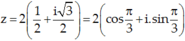
Do đó: 
Suy ra: ![]()
Vậy số phức w = (1 + i )z5 có phần thực là ![]() và phần ảo là
và phần ảo là ![]()
Tổng của phần thực và phần ảo là 32.
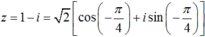
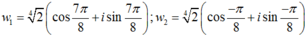
Chọn A.
Ta có:
có các căn bậc hai là