Cho hệ phương trình . Khẳng định nào sau đây là đúng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từ phương trình (1): x – my = m ⇔ x = m + my thế vào phương trình (2) ta được phương trình:
m (m + my) + y = 1
⇔ m 2 + m 2 y + y = 1 ⇔ ( m 2 + 1 ) y = 1 – m 2 ⇔ y = 1 − m 2 1 + m 2
(vì 1 + m 2 > 0 ; ∀ m ) suy ra x = m + m . 1 − m 2 1 + m 2 = 2 m 1 + m 2 với mọi m
Vậy hệ phương trình luôn có nghiệm duy nhất ( x ; y ) = 2 m 1 + m 2 ; 1 − m 2 1 + m 2
⇒ x – y = 2 m 1 + m 2 − 1 − m 2 1 + m 2 = m 2 + 2 m − 1 1 + m 2
Đáp án: B

=>2x+6y=2m+2 và 2x-y=7
=>7y=2m-5 và 2x-y=7
=>y=2/7m-5/7 và 2x=y+7
=>y=2/7m-5/7 và 2x=2/7m+30/7
=>x=1/7m+15/7 và y=2/7m-5/7
x0+2y0 bằng gì bạn ơi?

Đáp án C
Gọi ![]() là điểm cố định của họ đồ thị
(
C
m
)
, ta có
là điểm cố định của họ đồ thị
(
C
m
)
, ta có
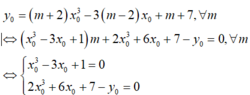
Vì hệ có 3 nghiệm phân biệt nên họ đồ thị có 3 điểm cố định.

Ta có: x + y = 4 x 2 + y 2 = m 2 ⇒ 4 2 − 2 P = m 2 ⇔ P = 16 − m 2 2
⇒ S 2 − 4 P = 16 − 2 16 − m 2 = 2 m 2 − 16 ≥ 0 ⇔ m ≥ 8
Đáp án cần chọn là: B

Dễ thấy hai phương trình đã cho có cùng tập nghiệm, cùng số nghiệm và tương đương nhưng không có cùng điều kiện xác định.
Đáp án cần chọn là: A

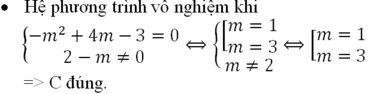


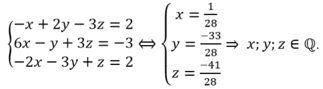
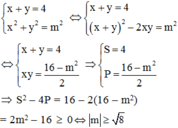
Đáp án A