So sánh hai luỹ thừa bằng cách tính giá trị cụ thể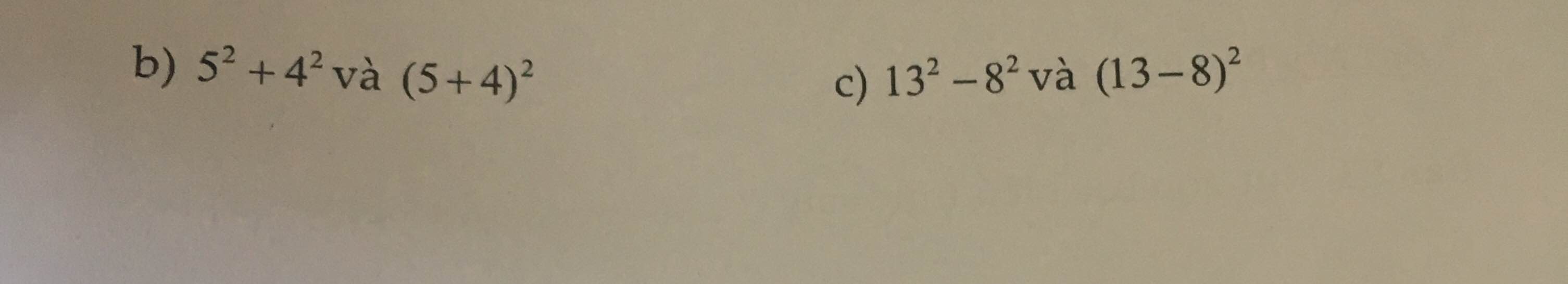
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
2
Những câu hỏi liên quan
1
DT
5
VM
25 tháng 9
Để tính giá trị của lũy thừa aba to the b-th power𝑎𝑏, bạn nhân số aa𝑎với chính nó bb𝑏lần. Ví dụ, 23=2×2×2=82 cubed equals 2 cross 2 cross 2 equals 823=2×2×2=8. Trong đó, aa𝑎là cơ số, còn bb𝑏là số mũ. Công thức: ab=a×a×…×a⏟blna to the b-th power equals modified a cross a cross … cross a with under brace below with b ln below𝑎𝑏=𝑎×𝑎×…×𝑎𝑏ln Các trường hợp đặc biệt:
- Số mũ 0: a0=1a to the 0 power equals 1𝑎0=1(với a≠0a is not equal to 0𝑎≠0).
- Số mũ âm: a−b=1aba raised to the negative b power equals the fraction with numerator 1 and denominator a to the b-th power end-fraction𝑎−𝑏=1𝑎𝑏. Ví dụ, 10-3=1103=11000=0.00110 to the negative 3 power equals the fraction with numerator 1 and denominator 10 cubed end-fraction equals 1 over 1000 end-fraction equals 0.00110−3=1103=11000=0.001.
- Cơ số 1: 1n=11 to the n-th power equals 11𝑛=1(với nn𝑛là số tự nhiên).
- Lũy thừa với số mũ tự nhiên - Lớp 6 - Vinastudy.vn a1=a. a0=1. 1n=1(n∈N) Vinastudy.vn
- Chương sách của Lũy thừa: Số mũ âm - Teachy Các số mũ âm là một sự mở rộng tự nhiên của ý tưởng về lũy thừa, một phép toán cơ bản trong toán học. Khi một số được nâng lên số ... teachy.ai
- 535 cubed53: (năm mũ ba): 5×5×5=1255 cross 5 cross 5 equals 1255×5×5=125.
- 434 cubed43: (bốn mũ ba): 4×4×4=644 cross 4 cross 4 equals 644×4×4=64.
- 10210 squared102: (mười mũ hai): 10×10=10010 cross 10 equals 10010×10=100.
CM
5 tháng 11 2018
A = 2019.2021 = (2018+1).2021 = 2018.2021 + 2021.
B = 2018.2022 = 2018.(2021+1) = 2018.2021+2018.
Vì 2018.2021+2021 >2018.2021+2018 nên A > B.
CM
17 tháng 2 2017
A = 2018.2018 - 2018.(2017+1) = 2018.2017 + 2018.
B = 2017.2019 = 2017.(2018+1) = 2017.2018 + 2017.
Vì 2018.2017 + 2018 > 2017.2018 + 2017 nên A > B.
26 tháng 9 2015
A = 198 . 202 B = 200 . 200
A = 198 . ( 200+ 2 ) B = (198 + 2 ) . 200
A = 198 . 200 + 198 . 2 B = 198 . 200 + 2 . 200
VI 198 . 2 < 2. 200 NEN A < B
19 tháng 10 2021
B=2010.2012=(2011-1).(2011+1)=2011.2011-1<2011.2011=A
B
23 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
b: \(5^2+4^2=25+16=41\)
\(\left(5+4\right)^2=9^2=81\)
mà 41<81
nên \(5^2+4^2< \left(5+4\right)^2\)
c: \(13^2-8^2=169-64=105\)
\(\left(13-8\right)^2=5^2=25\)
mà 105>25
nên \(13^2-8^2>\left(13-8\right)^2\)
\(b,\)\(5^2+4^2\)\(=25+16\) \(=41\)
\(\left(5+4\right)^2=9^2=81\)
\(mà\) \(41< 81\)
\(nên\) \(5^2+4^2< \left(5+4\right)^2\)