13 + 23 + 33 + ... + n3
=
Là 1 số chính phương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LT
0
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
Bài 1:
13 + 23 = 1 + 8 = 9 = 32 (là một số chính phương)
13 + 23 + 33 = 1 + 8 + 27 = 36 = 62 (là một số chính phương)
13 + 23 + 33 + 43 = 1 + 8 + 27 + 64 = 100 = 102 (là số cp)
13 + 23 + 33 + 43 + 53 = 1 + 8 + 27 + 64 + 125 = 225 = (15)2 là số cp
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
Bài 2:
1262 + 1 = \(\overline{..6}\) + 1 = \(\overline{...7}\) (không phải số chính phương)
100! + 8 = \(\overline{...0}\) + 8 = \(\overline{...8}\) (không phải là số chính phương)
1012 - 3 \(\overline{..01}\) - 3 = \(\overline{...8}\) (không phải là số chính phương)
107 + 7 = \(\overline{..0}\) + 7 = \(\overline{..7}\) (không phải là số chính phương)
11 + 112 + 113 = \(\overline{..1}\)+ \(\overline{..1}\)+ \(\overline{..1}\) = \(\overline{...3}\) (không phải số chính phương)
CM
30 tháng 3 2017
13 + 23 + 33 = 1 + 8 + 27 = 36.
Mà 36 = 62 là SCP (vì là bình phương của 6) nên 13 + 23 + 33 là SCP
CM
29 tháng 1 2018
13 + 23 + 33 + 43 = 1 + 8 + 27 + 64 = 100.
Mà 100 = 102 là SCP (vì là bình phương của 10) nên 13 + 23 + 33 + 43 là SCP.
Vậy mỗi tổng đã cho đều là số chính phương.
CM
4 tháng 9 2017
a, 3 2 + 4 2 = 25 = 5 2 là số chính phương.
b, 13 2 - 5 2 = 144 = 12 2 là số chính phương.
c, 1 3 + 2 3 + 3 3 + 4 3 = 100 = 10 2 là số chính phương.
CM
29 tháng 9 2019
Đặt vế trái bằng A n
Dễ thấy với n = 1 hệ thức đúng.
Giả sử đã có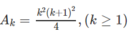 
Ta có:
CM
9 tháng 12 2019
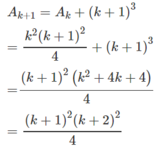
(SCP là viết tắt của số chính phương)
Ta có: 13 = 1; 23 = 8; 33 = 27; 43 = 64.
● 13 + 23 = 1 + 8 = 9.
Mà 9 = 32 là SCP (vì là bình phương của 3) nên 13 + 23 là SCP.
CM
18 tháng 9 2018
x + 1 3 + x + 2 3 + x + 3 3 = 0 ⇔ x + 1 3 + x + 2 3 = − x + 3 3 ⇔ x + 1 3 + x + 2 3 3 = − x + 3 3 3 ⇔ x + 1 + x + 2 + 3 ( x + 1 ) ( x + 2 ) 3 x + 1 3 + x + 2 3 = − x − 3
⇔ 3 ( x + 1 ) ( x + 2 ) 3 . ( − x + 3 3 − 3 x − 6
⇔ ( x + 1 ) ( x + 2 ) ( x + 3 ) 3 = x + 2
⇔ ( x + 1 ) ( x + 2 ) ( x + 3 ) = ( x + 2 ) 3
⇔ ( x + 2 ) ( x 2 + 4 x + 3 − x 2 − 4 x − 4 ) = 0
⇔ x + 2 = 0 ⇔ x = − 2
Thay x = - 2 lại phương trình ta thấy thỏa mãn
Vậy phương trình có nghiệm duy nhất x = - 2
Đáp án cần chọn là: D
LT
0